개요

  • 이 문서는 [[/study/think-bayes]] 책 43~49쪽을 공부한 내용이다.
  • 프레드릭 모스텔러(Frederick Mosteller)의 "모스텔러의 확률 고급 문제 50선과 해답"을 보면 기관차 문제가 있다.

각 철도에는 이를 지나가는 기관차에 1부터 N까지의 순서로 번호를 붙인다. 어느날 60호 기관차를 보았다. 이 때 이 철도에는 몇 개의 기관차가 지나가는지 추측해보자.

풀이

가설 세우기

이 문제는 [[dice-problem]]과 비슷하다.

주사위 문제의 풀이를 활용하기 위해 문제를 다음과 같이 생각할 수 있다.

  • 60 면체, 60 + 1 면체, 60 + 2 면체, … 60 + n 면체 주사위가 든 상자가 있다.
  • 상자에서 임의로 주사위 하나를 집어서 던졌더니 60이 나왔다.
  • 각 주사위를 선택했을 확률은?

가설과 데이터는 어떻게 될까?

  • n 개의 가설(Hypothesis)을 생각할 수 있다.
    • 가설 60 : 60면체 주사위를 던졌다.
    • 가설 61 : 61면체 주사위를 던졌다.
    • …
    • 가설 n : n 면체 주사위를 던졌다.
  • 데이터 D : 주사위를 던져 60이 나왔다.

표로 정리해 보면 다음과 같을 것이다.

식 설명 값
\(p(H_{60})\) n개의 주사위 중 60면체 주사위를 선택할 확률 \(\frac{1}{n}\)
\(p(H_{61})\) n개의 주사위 중 61면체 주사위를 선택할 확률 \(\frac{1}{n}\)
… … …
\(p(H_n)\) n개의 주사위 중 n면체 주사위를 선택할 확률 \(\frac{1}{n}\)
\(p(H_{1000})\) 1000개의 주사위 중 n면체 주사위를 선택할 확률 \(\frac{1}{1000}\)
\(p(D \mid H_{60})\) 60면체 주사위를 던져 60이 나올 확률 \(\frac{1}{60}\)
\(p(D \mid H_{61})\) 61면체 주사위를 던져 60이 나올 확률 \(\frac{1}{61}\)
… … …
\(p(D \mid H_{x})\) x면체 주사위를 던져 60이 나올 확률 \(\frac{1}{x}\)
\(p(D)\) 주사위를 던져 60이 나올 확률 아직 모름
  • 편의상 철도 회사가 보유한 총 기관차의 수가 n이라 하자.
    • 즉, \(p(H_{60})\)은 철도 회사가 보유한 n 대의 기관차 중 우리가 목격한 하나의 노선 위를 지나는 기관차가 60대일 확률이다.
    • 즉, 우리가 구하려 하는 것은 총 기관차 수 n 중에서 관찰 대상인 노선에서 운행되는 기관차의 수이다.

p(D)를 구하자

\(p(D)\)의 개념은 다음과 같다.

\[\begin{align} p(D) = & \space p(D \space and \space H_{60}) \\ & + p(D \space and \space H_{61}) \\ & + ... \\ & + p(D \space and \space H_{n}) \\ \end{align}\]

따라서 60면체에서 m면체까지 주사위가 전부 m - 59 개 있을 때, \(p(D)\)는 다음과 같다.

\[\begin{align} p(D) = & \space p(H_{m-59})p(D \mid H_{60}) \\ & + p(H_{m-59})p(D \mid H_{61}) \\ & + ... \\ & + p(H_{m-59})p(D \mid H_{m}) \\ \\ = & \space \frac{1}{m-59} \times \frac{1}{60} \\ & + \frac{1}{m-59} \times \frac{1}{61} \\ & + ... \\ & + \frac{1}{m-59} \times \frac{1}{m} \\ \\ = & \space \lim_{m \to \infty} \frac{1}{m-59} \left( \frac{1}{60} + \frac{1}{61} + ... + \frac{1}{m} \right) \\ = & \lim_{m \to \infty} \frac{1}{m-59} \sum_{k = 60}^{m} k^{-1} \\ \end{align}\]

한편, \(\sum_{k = 60}^{m} k^{-1}\)는 조화수(Harmonic number) \(H_m\) 이므로 이를 써서 다시 표기해보면 다음과 같이 표현할 수 있다.

\[p(D) = \lim_{m \to \infty} \frac{1}{m-59} \times \left( H_m - H_{59} \right)\]

그런데, n이 너무 커지면 곤란하기도 하고, 현실의 열차가 무한히 많을 수는 없으니 편의상 1000 까지만 따져 보도록 하자.

\[p(D) = \frac{1}{1000 - 59} \times \left( H_{1000} - H_{59} \right)\]

손으로 계산하기엔 시간이 너무 걸리므로 다음과 같이 간단한 자바스크립트 함수를 작성하여 계산해주자.

// 조화수 H_n 을 구한다
function harmonic(n) {
    if (n < 1) {
        throw "invalid argument";
    }
    if (harmonic[n] != null) {
        return harmonic[n];
    }
    if (n == 1) {
        return harmonic[1] = 1;
    }
    return harmonic[n] = harmonic(n - 1) + Math.pow(n, -1);
}
const p_d = (harmonic(1000) - harmonic(59)) / (1000 - 59);
console.log(p_d);

위의 코드를 실행해보면 다음과 같은 값이 출력된다.

\[p(D) \approx 0.0029992211628748922\]

사후 확률을 계산하자

이제 사후 확률을 계산할 수 있다.

[[Bayes-theorem]]에 의해 사후 확률은 다음과 같다. (단, \(x \ge 60\))

\[\begin{align} p(H_n \mid D) & = {p(H_n) \times p(D \mid H_n) \over p(D)} \\ & = {\frac{1}{1000-59} \times \frac{1}{n} \over p(D)} \\ & = {1 \over (1000-59) \times n \times p(D)}\\ & = {1 \over 941 \times n \times p(D)}\\ \end{align}\]

그렇다면 이제 모든 가설(열차가 60 대인 경우, 61 대인 경우, … n 대인 경우)을 비교하여 가장 가능성이 높은 가설을 찾아내기만 하면 된다.

즉, 다음 값들을 비교하여 가장 큰 값을 찾으면 된다.

\[\begin{matrix} p(H_{60} \mid D), & p(H_{61} \mid D), & ... \end{matrix}\]

그런데 n이 분모에 있으므로, n이 커질수록 수는 작아진다.

따라서 가능한 확률의 최대값이 나오는 n 은 60이 된다.

당연히 60대 중의 1대일 가능성이 61대 중의 1대일 가능성이나, 62대 중의 1대일 가능성보다 크기 때문이다.

코드를 짜서 사후확률을 계산해 보자

다음은 [[/study/think-bayes]]의 코드를 참고하여 자바스크립트로 풀어본 것이다.

// hypos: 가설의 배열
// 가설의 배열을 돌며 같은 경우의 수 1을 부여한다
function init(hypos) {
    const dict = {};
    hypos.forEach((h) => {
        dict[h] = 1;
    });
    return dict;
}

// 모든 가설을 돌며 mix의 data에 해당하는 값을 곱해 업데이트한다
function update(dict, data) {

    Object.keys(dict).forEach((hypo) => {
        dict[hypo] = dict[hypo] * likelihood(hypo, data);
    });

    return normalize(dict);
}

// p(D | H_n)
function likelihood(hypo, data) {
    if (hypo < data) {
        return 0;
    }
    return 1 / hypo;
}

// 모든 가설의 확률의 비율을 유지하며, 총합이 1이 되도록 정규화한다
function normalize(dict) {
    const values = Object.values(dict);
    const sum = values.reduce((a, b) => a + b);
    const result = {};
    Object.keys(dict).forEach((key) => {
        result[key] = dict[key] / sum;
    });
    return result;
}

function range(start, size) {
    return [...Array(size).keys()].map((n) => n + start);
}

function main() {
    const hypos = range(1, 1000);
    const pmf = init(hypos);
    const result = update(pmf, 60);

    Object.keys(result).forEach((k) => {
        console.log(k + '\t' + result[k])
    });
}

main();

위의 코드를 실행해서 엑셀에 붙여넣고 차트를 그려보면 다음과 같이 나온다.

$ node train.js | pbcopy

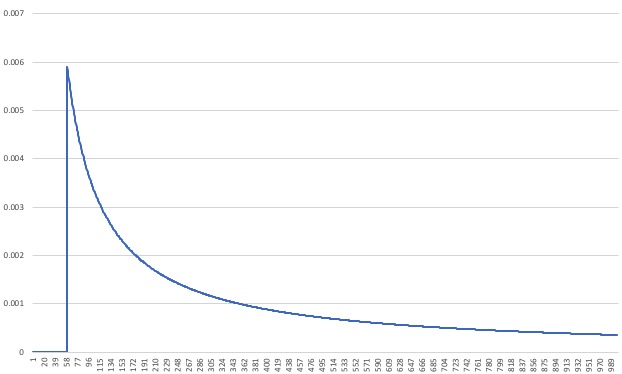
train-graph

기대값을 구해보자

하지만 원하는 값은 이런 결과가 아니므로 관점을 바꾸어 기대값, 즉 사후 확률의 평균을 구해 보도록 하자.

\[\begin{align} & 60 \times p(H_{60} \mid D) + 61 \times p(H_{61} \mid D) + ... + 1000 \times p(H_{1000} \mid D) \\ & = \frac{60}{941 \times 60 \times p(D)} + \frac{61}{941 \times 61 \times p(D)} + ... + \frac{1000}{941 \times 1000 \times p(D)} \\ & = \frac{1}{941 \times p(D)} + \frac{1}{941 \times p(D)} + ... + \frac{1}{941 \times p(D)} \\ & = 941 \times \frac{1}{941 \times p(D)} \\ & = \frac{1}{p(D)} \\ & \approx \frac{1}{0.0028222671142652737} \\ & \\ & \approx 333.41989326370776 \\ \end{align}\]

즉, 333대의 열차가 있을 것이라고 기대할 수 있다.

한편 위의 자바스크립트 코드 중 main함수만 다음과 같이 수정해주면 기대값을 구할 수 있다.

function main() {
    const hypos = range(1, 1000);
    const pmf = init(hypos);
    const result = update(pmf, 60);

    Object.keys(result).forEach((k) => {
        console.log(k + '\t' + result[k])
    });

    // 기대값 rs를 구한다
    const result2 = normalize(result);
    const rs = Object.keys(result2).reduce((a, b) => {
        return a + (b * result2[b])
    }, 0);
    console.log(rs);
}

위의 코드를 실행해보면 333.41989326371095가 나온다.

기대값을 구하는 공식을 만들어 보자

\(1 \over p(D)\)를 이용하면 되므로 공식으로도 만들 수 있을 것 같다.

  • a : 목격한 열차의 번호
  • b : 임의의 열차 번호 예상 최대값(위에서 1000으로 사용한 값)
\[\begin{align} \frac{1}{p(D)} & = \left( \frac{1}{b - (a - 1) } \times \left( H_b - H_{a - 1} \right) \right)^{-1}\\ & \\ & = {b - (a - 1) \over \sum_{k = a}^{b} k^{-1} } \\ \end{align}\]

WolframAlpha에 물어보자

공식을 만들었으니, 언제든지 WolframAlpha에 물어볼 수 있다.

사전 확률로 할 수 있는 것

균등 분포가 1 ~ 1000 일 때, 사후 확률의 평균은 333이 나왔다.

상한값이 500이라면 사후 확률 평균은 207일 것이고, 상한값이 2000이라면 사후 확률 평균은 552일 것이다.

function main(max) {
    const hypos = range(1, max);
    const pmf = init(hypos);
    let result = update(pmf, 60);

    const result2 = normalize(result);
    const rs = Object.keys(result2).reduce((a, b) => {
        return a + (b * result2[b])
    }, 0);
    console.log(rs);
}
main(500);  // 207.07922798340903
main(2000); // 552.179017164631

이런 방식으로는 상한값이 커질수록 사후 확률 평균도 커지게 되므로 바람직하지 않다.

따라서 데이터를 추가로 확보하면서 값이 조정되도록 해야 한다.

책에서는 60호 기관차에 이어 30번, 90번 기관차도 본 경우를 제시한다.

아마도 이런 경우의 사후 확률은 다음과 같이 식을 세우면 될 것 같다.

\[p(D | H_{60}) \times p(D | H_{30}) \times p(D | H_{90})\]

그렇다면 다음과 같이 계산할 수 있을 것이다.

function main(max) {
    const hypos = range(1, max);
    const pmf = init(hypos);

    // 60, 30, 90번 기관차를 목격
    let result = update(pmf, 60);
    result = update(pmf, 30);
    result = update(pmf, 90);

    const result2 = normalize(result);
    const rs = Object.keys(result2).reduce((a, b) => {
        return a + (b * result2[b])
    }, 0);
    console.log(rs);
}

main(500);  // 151.84958795903844
main(1000); // 164.30558642273365
main(2000); // 171.33818109150928

30, 90번 기관차를 본 데이터의 영향을 받아 사후 확률의 평균들의 차이가 줄었음을 알 수 있다.

상한선 60번 열차 사후평균 60, 30, 90 사후평균
500 약 207.08 약 151.85
1000 약 333.42 약 164.31
2000 약 552.18 약 171.34

사전 확률의 대안

  • 위와 같은 상황에서는 가급적이면 신뢰할 수 있는 데이터를 많이 수집하는 것이 좋다.
  • 철도 회사의 규모를 알아내기 위해 기관차 운송 분야 전문가와 인터뷰를 하는 것도 방법.

여기에서는 로버트 엑스텔(Robert Axtell)의 멱법칙을 사용해보도록 하자.

멱법칙 : 주어진 규모의 회사 크기는 규모의 분포의 역수이다.

\[PMF(x) \propto \left( \frac{1}{x} \right)^{a}\]

멱법칙 사전 확률을 고려하면 다음과 같이 init함수를 수정할 수 있다.

function init(hypos) {
    const dict = {};
    const alpha = 1
    hypos.forEach((h) => {
        dict[h] = Math.pow(h, -alpha);
    });
    return dict;
}

그리고 다음 코드를 다시 실행해보면 다음과 같은 결과가 나온다.

main(500);  // 130.70846986255998
main(1000); // 133.27523137503073
main(2000); // 133.99746308073068
상한선 60 사후평균 60,30,90 사후평균 멱법칙 적용 60,30,90
500 약 207.08 약 151.85 약 130.71
1000 약 333.42 약 164.31 약 133.28
2000 약 552.18 약 171.34 약 134.00

차이가 더 줄어들었음을 알 수 있다.

시험삼아 멱법칙 적용 코드에 hypos 값으로 2000000을 넣어봤더니 134.25418932762943가 나왔다.

숫자가 더 커져도 변동폭은 크지 않을 것으로 보인다.

신뢰구간 적용해보기

이번에는 위에서 계산한 분포 목록을 사용하여 90% 신뢰구간을 구해보자.

5분위와 95분위 값을 계산하면, 90% 신뢰구간을 구할 수 있다.

이미 normalize를 했기 때문에 그대로 순서대로 더해주기만 하면 되겠다.

  • 5분위 : 0~5% 에 해당하는 값을 모두 더해주면 된다.
  • 95분위 : 0~95% 에 해당하는 값을 모두 더해주면 된다.

다음과 같이 main 함수만 조금 고쳐주면 된다.

function main(max) {
    const hypos = range(1, max);
    const pmf = init(hypos);

    let result = update(pmf, 60);
    result = update(pmf, 30);
    result = update(pmf, 90);

    const result2 = normalize(result);

    const keys = Object.keys(result2);

    let p5 = 0;
    let p5total = 0;
    for(let i = 0; i < keys.length; i++) {
        const val = keys[i];
        const prob = result2[val];
        p5total += prob;
        if (p5total >= 0.05) {
            p5 = val;
            break;
        }
    }

    let p95 = 0;
    let p95total = 0;
    for(let i = 0; i < keys.length; i++) {
        const val = keys[i];
        const prob = result2[val];
        p95total += prob;
        if (p95total >= 0.95) {
            p95 = val;
            break;
        }
    }
    console.log({ '5%': p5, '95%': p95});
}

위의 코드를 실행해보면 다음과 같은 결과가 나온다.

main(500);  // { '5%': '91', '95%': '235' }
main(1000); // { '5%': '91', '95%': '242' }
main(2000); // { '5%': '91', '95%': '243' }

즉, (2000의 경우) 90% 신뢰구간은 (91, 243) 이다.

여기까지 공부했는데 약간 김 빠지긴 하지만 신뢰구간이 너무 넓어, 그닥 정확한 자료가 아님을 알 수 있다.

하긴 열차 3대만 목격했을 뿐인 상황에서 이정도면 꽤 놀라운 추정을 했다고는 볼 수 있겠다.

함께 읽기

  • [[Bayes-theorem]]
  • [[/study/think-bayes]]
  • [[/jargon/zipf-s-law]]
  • [[/jargon/copernican-principle]]