Clojure vector
Clojure Vector의 내부 구조를 알아보고 Java의 ArrayList와 비교한다
defn
(defn vector
"Creates a new vector containing the args."
{:added "1.0"
:static true}
([] [])
([a] [a])
([a b] [a b])
([a b c] [a b c])
([a b c d] [a b c d])
([a b c d e] [a b c d e])
([a b c d e f] [a b c d e f])
([a b c d e f & args]
(. clojure.lang.LazilyPersistentVector (create (cons a (cons b (cons c (cons d (cons e (cons f args))))))))))
Clojure collection으로서 vector의 특성
벡터는 coll?, counted?, sequential?, associative?로 검사했을 때 모두 true로 평가되는 유일한 Clojure collection 이다.
Examples
벡터는 []과 vector로 생성할 수 있다.
[] ; []
(vector) ; []
[1 2 3] ; [1 2 3]
(vector 1 2 3) ; [1 2 3]
벡터의 타입은 PersistentVector.
(type []) ; clojure.lang.PersistentVector
(class []) ; clojure.lang.PersistentVector
인덱스를 통한 벡터의 각 아이템 접근은 이렇게 한다.
; 벡터를 함수처럼 사용하고 인덱스를 넘기면 된다.
([:a :b :c] 0) ; :a
([:a :b :c] 1) ; :b
; nth나 get을 사용해도 된다.
(nth [:a :b :c] 0) ; :a
(nth [:a :b :c] 1) ; :b
(get [:a :b :c] 1) ; :b
(get [:a :b :c] 2) ; :c
길이는 count로 얻을 수 있다.
(count [:a :b :c]) ; 3
first, second, rest, last 모두 잘 작동한다. 단, rest는 ChunkedSeq 타입을 리턴한다.
(first [:a :b :c]) ; :a
(second [:a :b :c]) ; :b
(last [:a :b :c]) ; :c
(rest [:a :b :c]) ; (:b :c)
(type (rest [:a :b :c])) ; clojure.lang.PersistentVector$ChunkedSeq
앞에 값을 이어붙이는 cons는 리턴 타입이 Cons라는 점을 기억해두자.
벡터의 구조를 알고 있다면 앞에 붙이는 연산의 결과 리턴 타입이 vector가 아닌 이유를 어렵지 않게 알 수 있다.
(conj [:a :b :c] :tail) ; [:a :b :c :tail]
(cons :head [:a :b :c]) ; (:head :a :b :c)
(type (cons :head [:a :b :c])) ; clojure.lang.Cons
뒤에 값을 붙이는 conj는 타입이 바뀌지 않는다. 타입이 바뀌지 않는 이유는 아래의 PersistentVector 구현을 참고할 것.
(conj [:a :b :c] :d) ; [:a :b :c :d]
(type (conj [:a :b :c] :d)) ; clojure.lang.PersistentVector
assoc은 이렇게 쓴다.
(assoc [:a :b :c] 1 :foo) ; [:a :foo :c]
clojure.lang.PersistentVector
IPersistentVector의 구현체 중 하나인 clojure.lang.PersistentVector.
TransientVector: 인적 없는 숲에서 쓰러진 나무
PersistentVector의 정적 팩토리 메소드를 보면 TransientVector라는 타입을 볼 수 있다.
TransientVector는 PersistentVector의 내부 클래스이며, PersistentVector의 생성에 사용되는 특수한 구현이다.
(Clojure의 transient 개념에 대해서는 [[/clojure/reference/transient]] 문서 참고.)
clojure.lang.PersistentVector::create
static public PersistentVector create(List list){
int size = list.size();
if (size <= 32)
return new PersistentVector(size, 5, PersistentVector.EMPTY_NODE, list.toArray());
TransientVector ret = EMPTY.asTransient();
for(int i=0; i<size; i++)
ret = ret.conj(list.get(i));
return ret.persistent();
}
- size가 32 이하라면
new PersistentVector를 호출하며list.toArray()를 넘긴다.- 이렇게 넘겨준
list.toArray()는 새로 생성된PersistentVector의 tail이 된다.
- 이렇게 넘겨준
- 그러나 32를 초과한다면
TransientVector를 생성한다.asTransient()는return new TransientVector(this);.
items를 순회하며TransientVector의conj를 호출해item을 하나하나 붙여준다.- 이
conj는 매번 새로운 벡터를 생성하지 않는다.TransientVector의 상태를 바꿔가며 작업을 한다.
- 이
- 루프가 끝나면
TransientVector를PersistentVector로 변환해 리턴한다.
persistent()는 단순하게 arraycopy를 수행한 다음, new PersistentVector를 리턴한다.
public PersistentVector persistent(){
ensureEditable();
root.edit.set(null);
Object[] trimmedTail = new Object[cnt-tailoff()];
System.arraycopy(tail,0,trimmedTail,0,trimmedTail.length);
return new PersistentVector(cnt, shift, root, trimmedTail);
}
TransientVector는 PersistentVector를 생성하는 과정에서 퍼포먼스를 위해 임시로 생성하는 mutable한 자료구조로, 성능을 위해 선택된 방식이다.
단, TransientVector는 생성 과정에서만 사용되며, PersistentVector의 생성 결과로 공유되지는 않는다.
Clojure의 레퍼런스 문서Transient Data Structures( [[/clojure/reference/transient]]{한국어 번역} )에서는 이러한 TransientVector의 특성을 두고 재미있는 비유를 이야기한다.
If a tree falls in the woods, does it make a sound?
If a pure function mutates some local data in order to produce an immutable return value, is that ok?
만약 아무도 없는 숲 속에서 나무 한 그루가 쓰러졌다면, 과연 소리가 났을까?
만약 어떤 순수 함수가 변경 불가능한 리턴값을 생산하기 위해 로컬 데이터를 변경했다면, 올바른 일일까?
생성과 구조
PersistentVector 클래스를 열어보면 다음과 같은 멤버 필드들을 볼 수 있다.
final static AtomicReference<Thread> NOEDIT = new AtomicReference<Thread>(null);
public final static Node EMPTY_NODE = new Node(NOEDIT, new Object[32]);
final int cnt;
public final int shift;
public final Node root;
public final Object[] tail;
final IPersistentMap _meta;
public final static PersistentVector EMPTY =
new PersistentVector(0, 5, EMPTY_NODE, new Object[]{});
Node EMPTY_NODE: 비어있는 초기화된 노드. 길이는32.int cnt: 벡터의 길이.int shift: 벡터 내부의 트리를 순회하기 위한 비트 쉬프트 기준값. 5의 배수로 설정된다.Node root: 루트 노드.Object[] tail: 벡터의 꼬리.IPersistentMap _meta: 벡터의 메타 정보.
여기에 있는 root와 tail이 PersistentVector에 담겨 있는 아이템을 나누어 갖게 된다.
root는 각각 32개의 아이템을 갖는 배열의 배열이며, tail은 32개 까지의 아이템을 가질 수 있는 배열이다.
PersistentVector를 생성할 때 임시로 만든 TransientVector에 conj를 사용해 새로운 아이템을 계속해서 추가하게 된다.
이 때 tail은 일종의 버퍼 역할을 하는데 tail에 32개의 아이템이 들어가게 되면 tail이 root에 추가되는 방식으로 작동한다.
이 과정은 clojure.lang.PersistentVector::create(List list)의 return 문에
break point를 찍어두고 디버거를 켠 상태에서 벡터를 생성해보면 쉽게 관찰할 수 있다.
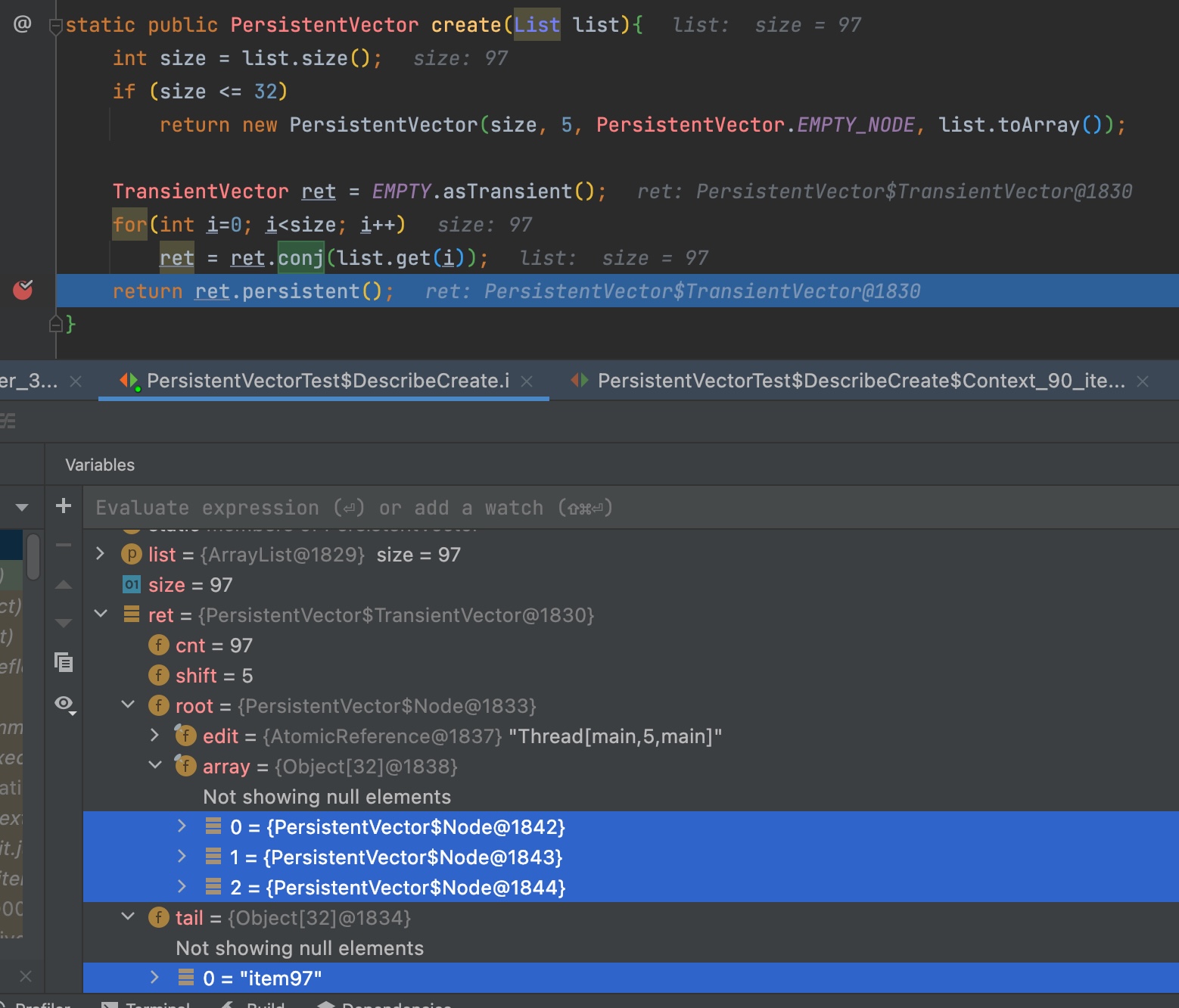
(스크린샷을 보면 임시로 생성한 TransientVector에 conj를 반복하고 있다.)
아래는 이렇게 90개의 아이템이 있는 경우를 내가 그림으로 그린 것이다.
만약 아이템이 96개라면 tail의 아이템이 32개로 꽉 차게 된다.
아이템이 1개 더 있는 97개라면 tail이 그대로 root[2]가 되며, 새로운 tail이 만들어진다.
그림 속의 새로 만든 tail은 마치 1칸만 갖고 있는 것 같지만 실제로는 32 사이즈를 갖는 배열이다.
이렇게 tail에 값을 할당하거나, tail을 root로 옮겨 달아주는 작업은 conj의 코드를 읽어보면 알 수 있다.
clojure.lang.PersistentVector::conj
public TransientVector conj(Object val){
ensureEditable();
int i = cnt;
// tail에 아직 공간이 남아있다면 아이템을 tail에 할당해준다.
if(i - tailoff() < 32)
{
tail[i & 0x01f] = val;
++cnt;
return this;
}
// tail의 32칸이 꽉 차있는 상태라면,
// tail을 root로 옮기고, tail을 새로 생성해야 한다.
// (이번에 추가하는 아이템은 새로 만든 tail에 할당해준다.)
Node newroot;
Node tailnode = new Node(root.edit, tail); // tail을 포함하고 있는 새로운 루트 노드
tail = new Object[32]; // 새로 만든 empty tail. 길이는 32.
tail[0] = val;
int newshift = shift;
if((cnt >>> 5) > (1 << shift)) // shift는 5의 배수이므로 > 의 오른쪽 항은 32^n
// 만약 root가 overflow 한다면 새로운 노드를 생성해 최상단 노드로 삼는다
{
newroot = new Node(root.edit);
newroot.array[0] = root;
newroot.array[1] = newPath(root.edit,shift, tailnode);
newshift += 5; // 새로운 최상단 노드가 생겼으므로 트리는 한 단계 높아졌다
}
else
// 만약 root에 아직 공간이 있다면 tail을 root에 달아준다
newroot = pushTail(shift, root, tailnode);
root = newroot;
shift = newshift; // 트리의 높이가 변하지 않았으므로 shift는 그대로 유지
++cnt; // 벡터에 아이템이 1개 추가되었으므로 cnt는 1 증가
return this;
}
root가 overflow 하게 되었을 때 newroot를 만들고, 기존의 root를 newroot의 [0]에 할당하는 부분이 흥미롭다.
트리의 높이가 한 단계 높아진 것이다.
shift와 newshift를 읽어보면 5씩 증가하는 값이라는 것을 알 수 있으므로, 이렇게 트리를 구성하는 기준도 32라는 것을 추측할 수 있다.
//overflow root?
if((cnt >>> 5) > (1 << shift))
{
newroot = new Node(root.edit);
newroot.array[0] = root;
newroot.array[1] = newPath(root.edit,shift, tailnode);
newshift += 5;
}
따라서 아이템이 97개인 경우에 대한 그림도 트리 구조로 다시 그릴 수 있다.
그리고 root 아이템의 수가 32를 초과하게 된다면 트리의 깊이도 깊어질 것이다.
이제 이걸 실험해 보자. 먼저 떠오르는 수는 1024와 1056이다.
아이템의 수가 1025개라면 다음과 같이 된다.
아이템의 수가 1056개라면 tail까지 꽉 차게 되며, 1057개가 되면 트리의 계층 구조가 한 단계 더 높아진다.
그림 속 root[1][0]을 핑크색으로 눈에 띄게 색칠한 이유는 해당 노드가 아이템의 수가 1056개일때까지는 tail이었다는 점을 강조하기 위해서이다.
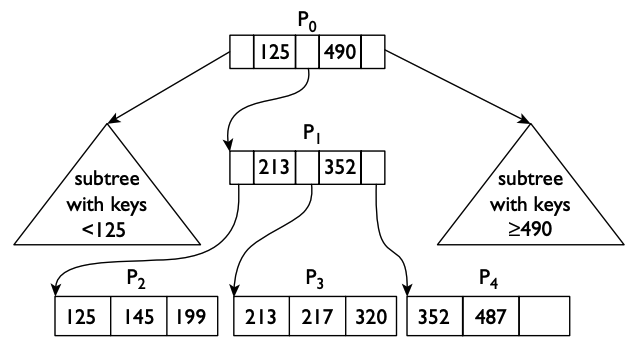
그런데 이 그림을 보다보면 차수가 32인 [[/algorithm/b-tree#b-plus-tree]]{B+ Tree}와 유사한 모양을 갖고 있다는 것도 알 수 있다.
PersistentVector는 불변성을 토대로 삼는 차수 32의 균형잡힌 B+ Tree의 일종으로 보인다.
트리의 높이
vector의 root부터 시작해서 리프에 있는 아이템에 도달하기까지의 array의 수를 트리의 높이라고 정의하자.
(공식 정의는 아니고 이 문서 안에서 편하게 이야기하기 위한 local 정의이다.)
90개의 아이템으로 구성된 벡터를 예로 들자면, vector.root부터 "item1"까지 array가 두 번 나타나므로 트리의 높이는 2 이다.
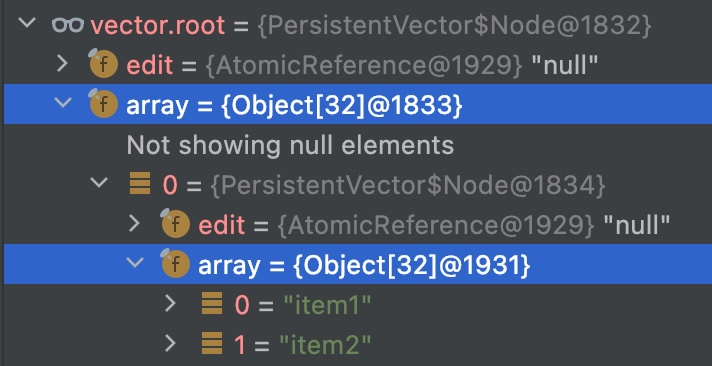
PersistentVector의 생성에 사용된 아이템의 수에 따른 트리의 높이를 실험해보니 다음과 같았다.
| 아이템의 수 | 트리의 높이 | tail 개수 | 아이템의 수 |
|---|---|---|---|
| 1 | 0 | 1 | \(1\) |
| 32 | 0 | 32 | \(32\) |
| 33 | 2 | 1 | \(32 + 1\) |
| 1,056 | 2 | 32 | \(32 ^ 2 + 32\) |
| 1,057 | 3 | 1 | \(32 ^ 2 + 32 + 1\) |
| 32,800 | 3 | 32 | \(32 ^ 3 + 32\) |
| 32,801 | 4 | 1 | \(32 ^ 3 + 32 + 1\) |
| 1,048,608 | 4 | 32 | \(32 ^ 4 + 32\) |
| 1,048,609 | 5 | 1 | \(32 ^ 4 + 32 + 1\) |
| 33,554,464 | 5 | 32 | \(32 ^ 5 + 32\) |
잘 살펴보면 규칙이 눈에 보인다. 다음과 같이 규칙에 따라 트리의 높이를 계산하는 식 \(f(n)\)을 만들어 보았다.
\[f(n) = \begin{cases} 0, & \text{if } \ 0 \le n \lt 33 \\ 2, & \text{if } \ 33 \le n \lt 65 \\ \floor{ \log_{32} (n-33) } + 1, & \text{if } \ 65 \le n \\ \end{cases}\]- 참고: \(0 \le n \lt 33\) 인 경우에는 아이템이 tail에만 있기 때문에 트리의 높이가 0 이다.
복잡해 보이지만 이진 트리의 높이 공식 \(\ceil{ \log_2 (n+1) }\)과 개념상으로 큰 차이가 없다. tail이 있기 때문에 조정값이 더 포함된 정도이다.
- 차수가 32인 트리이므로 log의 밑을 32로 삼았고, tail이 32개 초과시 root로 옮겨가니 \(-33\).
- \(\floor{ \ }\) 는 내림(floor)을 의미하며 트리의 높이를 자연수로 맞춰준다.
- \(+ 1\)은 트리 높이 숫자를 맞추기 위한 것.
이 함수를 Javascript로 간단하게 표현하자면 다음과 같다.
마지막 return문의 로그 계산은 \(\log_{32} (n-33) = \frac{ \log n-33 }{ \log 32 }\)이 되는 로그의 성질을 응용했다.
function calcHeight(cnt) {
if (0 <= cnt && cnt < 33) {
return 0;
} else if (33 <= cnt && cnt < 65) {
return 2;
}
return 1 + Math.floor(Math.log(cnt - 33) / Math.log(32));
}
아래의 입력칸에 아이템 수를 넣어보면 계산 결과를 볼 수 있다.
nth를 통한 랜덤 엑세스
아이템의 수가 65 이상일 때 트리의 높이가 \(\floor{ \log_{32} (n-33) } + 1\) 이므로 tail에 없는 아이템에 대한 랜덤 엑세스 퍼포먼스는 \(O( \log_{32} n )\) 이라는 것을 알 수 있다. (tail에 있는 아이템이라면 \(O(1)\).)
아이템의 수가 3355만 4465개가 되어도 높이가 6 밖에 안 된다. 벡터에 이정도까지 아이템을 많이 집어넣을 일은 흔하지 않다. (진짜로 넣을 일이 있다면 상황을 잘 판단해보고 그냥 C 스타일의 배열을 사용하는 것도 고려할 수 있을 것이다.) 랜덤 엑세스 퍼포먼스는 괜찮은 편이다.
아래는 랜덤 엑세스를 제공해주는 nth이다.
clojure.lang.PersistentVector::nth
public Object nth(int i){
ensureEditable(); // TransientVector 라면 예외를 던진다
Object[] node = arrayFor(i);
return node[i & 0x01f];
}
읽어보면 arrayFor에 인덱스값을 넘겨 배열을 받아오는데, 이건 해당 인덱스의 아이템이 포함되어 있는 노드 하나를 가져오는 작업이다.
노드 하나는 다음과 같이 가져온다.
private Object[] arrayFor(int i){
if(i >= 0 && i < cnt)
{
if(i >= tailoff())
return tail;
Node node = root;
for(int level = shift; level > 0; level -= 5)
node = (Node) node.array[(i >>> level) & 0x01f];
return node.array;
}
throw new IndexOutOfBoundsException();
}
- 인덱스
i가tailoff()이상이면tail을 리턴한다. - 그렇지 않다면
root노드의 깊이를 타고 내려가서 (이 과정에서for루프가 사용된다) 해당 인덱스가 포함된 노드를 리턴한다.
불변성을 활용한 노드의 공유
PersistentVector는 불변성을 보장하는 자료구조이기 때문에, 벡터를 이루는 각 아이템 값의 업데이트를 지원하지 않는다.
즉 한 인덱스의 값을 바꾸는 것이 필요하다면 값 하나만 다른, 복제된 벡터를 만들어야 하는 방식이다.
그러나 그렇다고 해서 PersistentVector는 모든 아이템을 array copy하는 방식이 아니라,
해당 아이템이 포함되어 있는 노드(길이가 32인 배열)만 새로 생성하고 벡터의 나머지는 원본 벡터의 다른 노드들을 참조하는 방식을 사용한다.
이 작업을 이해하기 위해 assocN 메소드를 살펴보자.
clojure.lang.PersistentVector::assocN
public PersistentVector assocN(int i, Object val){
if(i >= 0 && i < cnt)
{
if(i >= tailoff())
{
// assoc 하려는 인덱스가 tail에 있다면 새로운 복제 tail을 만든다.
Object[] newTail = new Object[tail.length];
System.arraycopy(tail, 0, newTail, 0, tail.length);
// 복제한 새로운 tail의 목표 인덱스의 값을 업데이트한다.
newTail[i & 0x01f] = val;
// 새로운 tail을 달고 있고, 나머지 노드는 그대로 연결되어 있는 벡터를 리턴한다.
return new PersistentVector(meta(), cnt, shift, root, newTail);
}
// assoc 하려는 인덱스가 노드 중에 있다면...
return new PersistentVector(meta(), cnt, shift, doAssoc(shift, root, i, val), tail);
}
if(i == cnt)
return cons(val);
throw new IndexOutOfBoundsException();
}
private static Node doAssoc(int level, Node node, int i, Object val){
// 목표 노드의 복제 노드
Node ret = new Node(node.edit,node.array.clone());
if(level == 0)
{
// 목표 노드가 맞다면 목표 인덱스의 값을 업데이트한다.
ret.array[i & 0x01f] = val;
}
else
{
// 목표 노드가 아니라면 재귀하며 노드 연결 작업.
// level은 shift 값으로 5씩 감소시킨다.
int subidx = (i >>> level) & 0x01f;
ret.array[subidx] = doAssoc(level - 5, (Node) node.array[subidx], i, val);
}
// 작업이 끝난 복제 노드를 리턴한다.
return ret;
}
앞에서 살펴봤던 1057개의 아이템이 있는 벡터에서 item1056만 item1056 updated로 편집된 벡터가 필요하다고 하자.
이럴 때 assocN을 사용하면 다음과 같은 벡터가 생성되어 리턴된다. 새로 생성된 벡터의 root[0]은 이전 벡터의 root[0]과 같은 배열을 공유한다.
(이 그림에서 tail은 그리기 귀찮아서 생략하였다.)2
즉 리프 노드 아이템은 item1025부터 item1055까지의 31개만 복사되었고, 나머지는 원본의 노드를 참조하는 방식으로 해결되었다.
PersistentVector는 불변성을 토대로 하고 있기 때문에 이렇게 내부 구조를 이루고 있는 노드들을 다른 자료구조와 부담없이 공유할 수 있다.
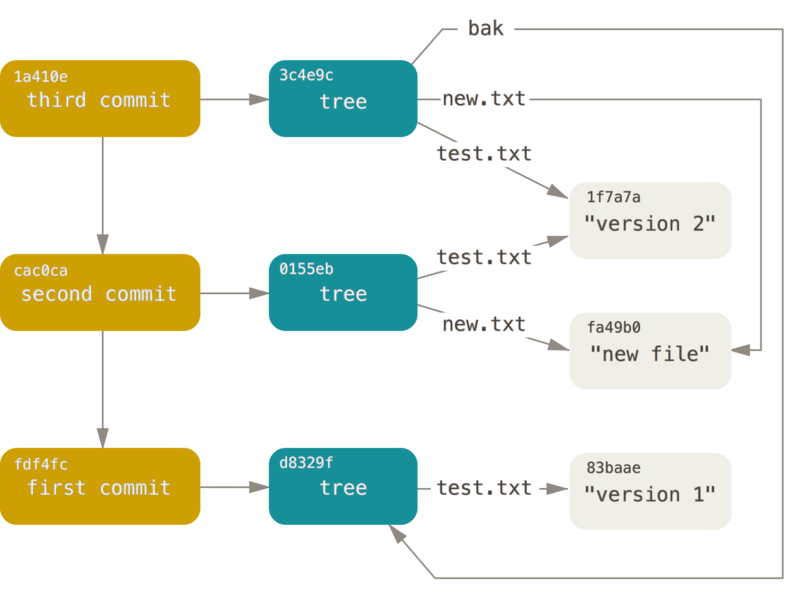
한편 불변성을 토대로 삼는 트리 구조라는 특성 때문에 가능한 자연스러운 노드 공유는 git의 핵심 기법이기도 하다.
위의 그림은 git 데이터 모델의 예제로, version 2와 new file이라는 blob을 3c4e9c와 0155eb라는 두 트리가 참조하고 있는 상황을 보여준다.
이렇게 두 트리가 같은 blob을 안심하고 참조하는 것이 가능한 이유는 git의 blob이 immutable하기 때문이다.
git의 DB가 update와 delete를 허용하지 않기 때문에 git의 트리는 PersistentVector와 구조적 공통점을 갖게 된 셈이다.
git의 DB와 JVM의 heap을 blob 저장소라는 개념으로 본다면 이런 그림도 떠올릴 수 있을 것이다.
java.util.ArrayList와의 비교
반면 [[/java/arraylist]]는 mutable하기 때문에 두 ArrayList가 아이템을 공유하면 다양한 문제가 발생할 수 있다.
다음 그림은 ArrayList가 내장하는 배열의 주소를 다른 ArrayList가 참조하는 배열의 중간에 연결되는 가상의 상황을 추상적으로 그린 것이다.
ArrayList는 mutable하므로 온갖 재앙이 터져나올 것이다. 그러므로 ArrayList는 이렇게 설계되지 않았다. 하지만 이건 ArrayList의 결함이나 단점이 아니라 ArrayList가 Dynamic Array의 구현이기 때문이다. 구조와 컨셉이 다르기 때문에 자료구조의 사용 방법이 다른 것이지 ArrayList에 문제가 있는 것은 아니다.
Java의 ArrayList는 최종적으로 추가되는 아이템의 수를 초기화 시점에 알고있는지에 따라 성능상에 차이가 크다.
ArrayList는 grow factor를 1.5로 삼고 있는 Dynamic Array의 구현체이므로 grow의 횟수를 잘 제어할 수 있는지 없는지에 따라 생성 퍼포먼스가 크게 차이날 수 있다.
소멸할 때까지 contain하는 아이템의 수가 결정되어 있다면, \(O(n)\)의 성능을 보인다. 그러나 몇 개를 추가하게 될 지 알 수 없다면 이야기가 다르다.
ArrayList의 DEFAULT_CAPACITY는 10인데,
하나씩 하나씩 아이템을 추가하게 되면 1.5배의 capacity를 갖는 새로운 배열을 생성하고, 그 배열로 array copy를 한다.
private Object[] grow(int minCapacity) {
int oldCapacity = elementData.length;
if (oldCapacity > 0 || elementData != DEFAULTCAPACITY_EMPTY_ELEMENTDATA) {
// 일반적으로 새 capacity는 oldCapacity + (oldCapacity / 2)
int newCapacity = ArraysSupport.newLength(oldCapacity,
minCapacity - oldCapacity, /* minimum growth */
oldCapacity >> 1 /* preferred growth */);
return elementData = Arrays.copyOf(elementData, newCapacity);
} else {
return elementData = new Object[Math.max(DEFAULT_CAPACITY, minCapacity)];
}
}
만약 다수의 아이템을 ArrayList에 집어넣으려 할 때의 최악의 케이스는 다음과 같이 아이템을 하나하나 추가하는 것이다.
final List<Integer> numbers = new ArrayList<>();
for (int i = 0; i < 32801; i++) {
numbers.add(i);
}
32801개의 아이템을 하나씩 일일이 ArrayList에 추가할 때 내부에서 새로 만드는 배열의 사이즈를 순서대로 나열해보면 다음과 같다.
10, 15, 22, 33, 49, 73, 109, 163, 244, 366, 549, 823, 1234, 1851, 2776, 4164, 6246, 9369, 14053, 21079, 31618, 47427 4
array copy를 통한 아이템의 복사는 146,029 회.5
\[10 + 15 + ... + 31618 + (32801 - 31618) = 146029\]그러므로 32801개의 아이템을 ArrayList에 하나 하나 추가하면 최소한 146029회의 값 복사가 발생한다. (게다가 복제 이후에 이전의 배열은 안 쓰게 되므로 gc가 모두 청소할 것이다.) 비트 연산으로 인한 1 비트 무조건 내림을 고려하지 않는다면 단순 [[/study/rosen-discrete-math-7/summations]]{등비수열의 합}으로 소박하게 표현하는 것도 가능하다.
아이템의 수를 n 이라 하면 grow의 발생 횟수 \(G_n\)을 다음과 같이 생각할 수 있다. (아이템의 수가 11일 때 grow가 최초 발생한다는 전제)
\[G_n = \ceil{ \log_{1.5} ( { n \over 10 }) }\]n = 47427 인 경우의 \(G_n\) (www.wolframalpha.com)
그러므로 복사 횟수는 아이템의 수가 10 이상일 경우 대충 다음과 같을 것이다.
\[\begin{align} S_n & = { 10 ( 1.5^{G_n} - 1 ) \over 1.5 - 1 } \\ & = 20 ( 1.5^{G_n} - 1 ) \\ & = 20 ( 1.5^{ \ceil{ \log_{1.5} ( { n \over 10 }) } } - 1 ) \\ \end{align}\]식으로 따지면 복잡하니 32801개의 아이템이 있을 때 146029회의 값 복사가 예상된다는 것에 주목하자. 그러나 이것은 ArrayList를 멍청하게 사용한 방법이기 때문에 그렇다.
ArrayList는 몇 개의 아이템을 추가할 지 결정하면 최적의 생성 finalize 성능을 보이는데, initialCapacity를 지정해 생성하면 내부 배열의 사이즈를 확정할 수 있기 때문이다.
public ArrayList(int initialCapacity) {
이 생성자를 사용하고 capcity를 초과하는 아이템을 더 넣지만 않는다면, array copy를 하지 않기 때문에 \(O(n)\)의 성능을 보인다.
TransientVector를 사용해 생성되는 PersistentVector는 아이템을 추가했을 때 array copy를 사용하지 않는다. 아이템이 많아도 각 tail을 트리에 연결해주는 작업만 하면 된다.
tail은 32개가 될 때마다 꽉 차며 33번째 아이템이 추가되려 할 때 트리에 연결되므로, tail의 레퍼런스가 트리에 연결된 횟수는 대략 \(\frac{ 32801 }{ 32 }\). 약 1025 회에 가깝다. ArrayList에 32801개의 아이템을 집어넣을 때 아이템 복사가 14만회 이상 수행된다는 추정을 떠올려보자.
APersistentVector의 subvec을 통한 순서 있는 부분집합의 생성
PersistentVector는 APersistentVector에서 상속받은 subList를 통해 순서가 유지되는 부분집합을 제공하는데,
subList는 RT의 subvec을 호출하고, RT의 subvec은 APersistentVector의 SubVector를 생성하게 된다.
다음은 SubVector의 생성자이다.
clojure.lang.APersistentVector.SubVector
public SubVector(IPersistentMap meta, IPersistentVector v, int start, int end){
this._meta = meta;
if(v instanceof APersistentVector.SubVector)
{
APersistentVector.SubVector sv = (APersistentVector.SubVector) v;
start += sv.start;
end += sv.start;
v = sv.v;
}
this.v = v;
this.start = start;
this.end = end;
}
코드를 보면 SubVector는 시작점과 끝점을 갖고 있는 벡터 v의 wrapper이다.
그래서 nth도 start를 활용해 작동한다.
clojure.lang.APersistentVector.SubVector::nth
public Object nth(int i){
if((start + i >= end) || (i < 0))
throw new IndexOutOfBoundsException();
return v.nth(start + i);
}
Cons와 ChunkedSeq
cons를 벡터에 사용하면 Cons 타입의 인스턴스가 리턴된다.
(cons 777 [666])
=> (777 666)
(type (cons 777 [666]))
=> clojure.lang.Cons
(type (rest (cons 777 [666])))
=> clojure.lang.PersistentVector$ChunkedSeq
이건 위에서 살펴본 벡터의 구조상 앞에 뭔가를 추가했을 때 트리구조를 전부 재구성하지 않기 위해 벡터를 래핑하는 Cons를 사용하고 있는 것이다.
static public ISeq cons(Object x, Object coll){
//ISeq y = seq(coll);
if(coll == null)
return new PersistentList(x);
else if(coll instanceof ISeq)
return new Cons(x, (ISeq) coll);
else
return new Cons(x, seq(coll)); // 벡터에 cons를 쓰면 여기로 온다
}
Cons의 생성자는 굉장히 심플하며, more가 있는 것으로 보아 연결 리스트처럼 작동한다는 것도 알 수 있다.
public Cons(Object first, ISeq _more){
this._first = first;
this._more = _more;
}
Cons의 메소드들은 매우 심플하므로 이해하기도 어렵지 않다.
public Object first(){
return _first;
}
public ISeq next(){
return more().seq();
}
public ISeq more(){
if(_more == null)
return PersistentList.EMPTY;
return _more;
}
public int count(){
return 1 + RT.count(_more);
}
한편 벡터에 rest를 사용했을 때 리턴되는 타입인 ChunkedSeq 또한 Cons처럼 벡터의 wrapper이다.
clojure.lang.PersistentVector.ChunkedSeq
public ChunkedSeq(PersistentVector vec, int i, int offset){
this.vec = vec;
this.i = i;
this.offset = offset;
this.node = vec.arrayFor(i);
}
arrayFor를 사용해 PersistentVector의 특정 노드를 root로 선정한 다음, i와 offset을 활용해 인덱스를 보정해 다양한 오퍼레이션에 대응하는 방식이다.
public Object first(){
return node[offset];
}
public int count(){
return vec.cnt - (i + offset);
}
Clojure 컴파일러의 벡터 생성
Compiler::compile 메소드의 시그니처는 다음과 같다.
clojure.lang.Compiler::compile
public static Object compile(
Reader rdr, String sourcePath, String sourceName) throws IOException {
시그니처를 읽어보면 소스코드 파일 패스와 이름을 받아서 Reader로 읽고 뭔가를 한다는 것을 알 수 있다.
30줄 정도 더 내려가보자. objx의 internalName과 objtype을 결정하는 곳이 보인다.
아직 objx는 초기화만 되어 있는 상태라고 볼 수 있다.
clojure.lang.Compiler::compile
ObjExpr objx = new ObjExpr(null);
objx.internalName = sourcePath.replace(File.separator, "/").substring(0, sourcePath.lastIndexOf('.'))
+ RT.LOADER_SUFFIX;
objx.objtype = Type.getObjectType(objx.internalName);
이후 LispReader가 form을 읽고, compile1 메소드로 objx와 form을 넘겨준다.
for(Object r = LispReader.read(pushbackReader, false, EOF, false, readerOpts); r != EOF;
r = LispReader.read(pushbackReader, false, EOF, false, readerOpts))
{
LINE_AFTER.set(pushbackReader.getLineNumber());
COLUMN_AFTER.set(pushbackReader.getColumnNumber());
compile1(gen, objx, r);
LINE_BEFORE.set(pushbackReader.getLineNumber());
COLUMN_BEFORE.set(pushbackReader.getColumnNumber());
}
compile1은 form을 분석하고 expression을 생성한 다음, 넘겨받은 objx에 대해 emit을 실행한다.
Expr expr = analyze(C.EVAL, form);
objx.keywords = (IPersistentMap) KEYWORDS.deref();
objx.vars = (IPersistentMap) VARS.deref();
objx.constants = (PersistentVector) CONSTANTS.deref();
expr.emit(C.EXPRESSION, objx, gen);
expr.eval();
Expr은 인터페이스이고, Expr의 벡터 구현체는 VectorExpr 이다. 그러므로 다음 메소드 emit이 실행된다.
clojure.lang.Compiler.VectorExpr::emit
public void emit(C context, ObjExpr objx, GeneratorAdapter gen){
if(args.count() <= Tuple.MAX_SIZE)
{
for(int i = 0; i < args.count(); i++) {
((Expr) args.nth(i)).emit(C.EXPRESSION, objx, gen);
}
gen.invokeStatic(TUPLE_TYPE, createTupleMethods[args.count()]); // 여기
}
else
{
MethodExpr.emitArgsAsArray(args, objx, gen);
gen.invokeStatic(RT_TYPE, vectorMethod); // 여기
}
if(context == C.STATEMENT)
gen.pop();
}
// 여기라고 표시한 부분을 보면 createTupleMethods와 vectorMethod가 보인다.
createTupleMethods의 정의는 다음과 같다.
final static Method createTupleMethods[] = {Method.getMethod("clojure.lang.IPersistentVector create()"),
Method.getMethod("clojure.lang.IPersistentVector create(Object)"),
Method.getMethod("clojure.lang.IPersistentVector create(Object,Object)"),
Method.getMethod("clojure.lang.IPersistentVector create(Object,Object,Object)"),
Method.getMethod("clojure.lang.IPersistentVector create(Object,Object,Object,Object)"),
Method.getMethod("clojure.lang.IPersistentVector create(Object,Object,Object,Object,Object)"),
Method.getMethod("clojure.lang.IPersistentVector create(Object,Object,Object,Object,Object,Object)")
};
vectorMethod는 이러하다.
final static Method vectorMethod = Method.getMethod("clojure.lang.IPersistentVector vector(Object[])");
즉, clojure.lang.IPersistentVector의 정적 팩토리 메소드의 시그니처를 String으로 표현한 것을 getMethod를 통해 Method로 확보하고 있는 것이다.
잘 읽어보면 배열의 인덱스(0 ~ 6)이 인자의 수와 일치한다는 것도 알 수 있다.
아마도 벡터 표현식에 포함된 인자의 수를 통해 벡터를 생성하는 메소드에 접근할 것이다.
한편 이 메소드들은 clojure.lang.Tuple 클래스에 정의된 것들이다.
public class Tuple{
static final int MAX_SIZE = 6;
public static IPersistentVector create(){return PersistentVector.EMPTY;}
public static IPersistentVector create(Object v0)
{return RT.vector(v0);}
public static IPersistentVector create(Object v0, Object v1)
{return RT.vector(v0, v1);}
public static IPersistentVector create(Object v0, Object v1, Object v2)
{return RT.vector(v0, v1, v2);}
public static IPersistentVector create(Object v0, Object v1, Object v2, Object v3)
{return RT.vector(v0, v1, v2, v3);}
public static IPersistentVector create(Object v0, Object v1, Object v2, Object v3, Object v4)
{return RT.vector(v0, v1, v2, v3, v4);}
public static IPersistentVector create(Object v0, Object v1, Object v2, Object v3, Object v4, Object v5)
{return RT.vector(v0, v1, v2, v3, v4, v5);}
}
함께 읽기
- [[/study/rosen-discrete-math-7/summations]]
- [[/java/arraylist]]
- 이 글을 작성하기 위해 만든 테스트 코드
참고문헌
- https://clojuredocs.org/clojure.core/vector
- Collections and Sequences in Clojure (www.brainonfire.net)
- Dynamic array (wikipedia.org)
- Pro Git 10.2 Git Internals - Git Objects (git-scm.com)
- Understanding Clojure's Persistent Vectors, pt. 1
- Understanding Clojure's Persistent Vectors, pt. 2
- Understanding Clojure's Persistent Vectors, pt. 3
- clojure 1.11.0-alpha4 소스코드 (github.com)
- openjdk/jdk jdk-19+6 (github.com)
- 트랜잭션 처리의 원리 / 필립 A. 번스타인, 에릭 뉴코머 공저 / 한창래 역 / KICC(한국정보통신) / 1판 1쇄 2011년 12월 19일
참고사항
- 이 글은 2022년 1월 26일 수요일 그린랩스 사내 세미나 발표 자료로 활용되었음.
주석
-
트랜잭션 처리의 원리. 6.9 B-Tree 잠금. 225쪽. ↩
-
Understanding Clojure's Persistent Vectors, pt. 1 문서를 참고하면 이와 관련된 풍부한 설명을 읽을 수 있다. ↩
-
Pro Git 10.2장에 포함된 그림 149. ↩
-
이 목록은 vim 매크로로 생성했다. 사용한 매크로는
"ayiwo^R=@a*1.5^M<Esc>0이다. ↩ -
vim substitute를 사용해
,를+로 바꾸고 vim command line에서:!bc로 계산하였다. ↩