빅 오 표기법(Big O notation)
알고리즘의 효율성을 나타내는 표기법이다
기원
big-O 표기의 역사
big-O 표기는 한 세기 이상 수학에서 사용되어 왔다. 3.3절에서 보겠지만 컴퓨터과학에서는 알고리즘 분석에 광범위하게 사용된다. 독일의 수학자 Paul Bachmann이 1892년 처음으로 big-O 표기를 정수론에 관한 책에서 사용하였다. 그의 저술에서 두루 이 표기를 사용한 수학자 Edmund Landau의 이름을 따서 때로는 big-O 기호를 Landau symbol이라 부르기도 한다. 컴퓨터과학에서 big-O 표기는 Donald Knuth에 의해 널리 사용되기 시작했는데, 나중에 이 절에서 소개할 big-Ω와 big-Θ도 그에 의해 소개되었다.
– Rosen의 이산수학. 3.2장. 233쪽.
요약
- O
빅-오라고 읽는다.- 점근적 상한에 대한 표기법.
- \(O(g(n))\)은 \(g(n)\)의 증가율보다 작거나 같은 함수들의 집합이다.
- 예를 들어 \(O(n^2)\)에는 \(O(1), O(n), O(n \log n)\) 등이 포함된다.
- 주어진 알고리즘의 증가율보다 크거나 같은 최소의 증가율을 찾는 것이 목적.
- Ω
빅-오메가라고 읽는다.- 점근적 하한에 대한 표기법.
- 주어진 알고리즘의 증가율보다 작거나 같은 최대의 증가율을 찾는 것이 목적.
- Θ
빅-세타라고 읽는다.- 이 표기법은 주어진 함수(알고리즘)의 상한과 하한이 같은지 아닌지를 결정한다.
- 세타(Θ) 표기법은 항상 상한(O)과 하한(Ω) 사이에 존재한다.
- 상한과 하한이 같다면, 세타 표기법도 같은 증가율을 갖는다.
최선의 경우, 최악의 경우, 평균의 경우를 분석할 때 상한(O), 하한(Ω), 평균 수행 시간(Θ)을 구하려 한다. 앞의 예에서 알 수 있듯이, 주어진 함수(알고리즘)가 상한(O)과 하한(Ω)을 가진다고 해서 평균 수행 시간(Θ)이 항상 가능한 것은 아니라는 것이 분명하다. 예를 들어 어떤 알고리즘의 최선의 경우를 논의한다면 상한(O)과 하한(Ω)과 평균 수행 시간(Θ)을 구하려 하는 것이다. 이 장의 나머지 부분에서는 상한(O)에 집중할 텐데 왜냐하면 알고리즘의 하한(Ω)을 아는 것은 실용적으로 중요하지 않으며 상한(O)과 하한(Ω)이 같을 경우에는 세타 표기법을 사용하기 때문이다.
– 다양한 예제로 학습하는 데이터 구조와 알고리즘 for Java. 1장. 15쪽.
- 알고리즘을 분석할 때 상한(O), 하한(Ω), 평균 수행 시간(Θ)을 구한다.
- O와 Ω가 같을 때에는 Θ을 쓴다.
함수의 증가를 설명하기 위하여 big-O가 광범위하게 사용되나 한계가 있다. 특히, f(x)가 O(g(x))일 때, 충분히 큰 x에 대하여 g(x)에 의해 f(x)의 상한이 주어진다. big-O는 충분히 큰 x에 대하여 f(x)의 크기에 대한 하한이 주어지지는 않는다. 이 하한을 제공하기 위하여 big-Omega 표기를 사용한다. 참조함수 g(x)에 관하여 함수 f(x)의 크기에 대한 상한과 하한을 동시에 나타내기 위하여 big-Theta 표기가 사용된다. big-Omega와 big-Theta 표기는 1970년대에 Donald Knuth에 의해 소개되었다. 이 표기를 도입한 동기는 함수의 크기에 대한 상한과 하한이 모두 필요한 경우에 big-O를 잘못 사용하기 때문이었다.
– Rosen의 이산수학. 3.2장. 242쪽.
big-O와 big-Omega 표기 사이에는 밀접한 관련성이 있다. 특히, f(x)가 Ω(g(x))인 것은 g(x)가 O(f(x))가 되기 위한 필요충분조건이다.
– Rosen의 이산수학. 3.2장. 243쪽.
비고: f(x)가 O(g(x))라는 사실을 때때로 f(x) = O(g(x))로 표시한다. 하지만, 이 표시에서
=은 동등함을 의미하는 것은 아니다. 오히려 이 표시는 정의역의 충분히 큰 값에 대해서 함수 f와 g의 값이 같지 않다는 것을 의미한다. 그러나 f(x) ∈ O(g(x))라고 할 수 있다. 왜냐하면 O(g(x))가 O(g(x))인 함수의 집합을 표현하기 때문이다.f(x)가 O(g(x))이고, h(x)가 충분히 큰 x에 대하여 g(x)보다 큰 절대값을 갖는 함수일 때 f(x)는 O(h(x))이다. 다시 말해, f(x)가 O(g(x))인 관계에서 함수 g(x)는 보다 큰 절대값을 갖는 함수로 대치될 수 있다. 이 사실은 다음으로부터 알 수 있다.
만약 \(x \gt k\)일 때, \(\vert f(x) \vert \le C \vert g(x) \vert\) 이고
그리고 모든 \(x \gt k\)에 대해, \(\vert h(x) \vert \gt \vert g(x) \vert\)이면
\(x \gt k\)일 때, \(\vert f(x) \vert \le C \vert h(x) \vert\) 이다.
그러므로 f(x) 는 O(h(x))이다.
big-O 표기가 사용될 때, f(x)가 O(g(x))인 관계에 등장하는 함수 g는 가능한 한 작은 것을 선택해야 한다(때로는 양의 정수 n에 대해, \(x^n\)형태의 함수와 같은 참조함수의 집합으로부터). 1
big-O
Definition.
Let \(f\) and \(g\) be functions from the set of integers or the set of real numbers to the set of real numbers. We say that \(f(x)\) is \(O(g(x))\) if there are constants \(C\) and \(k\) such that
\(\vert f(x) \vert \le C \vert g(x) \vert\)
whenever \(x \gt k\). [This is read as "\(f(x)\) is big-oh of \(g(x)\)."] 1
함수 \(f\)와 함수 \(g\)가 정수(or 실수)의 집합으로부터 실수의 집합으로의 함수라 하자.
\(x \gt \color{red}k\) 일 때, \(\vert f(x) \vert \le \color{red}C \vert g(x) \vert\) 를 만족하는 상수 \(C, k\) 가 존재하면,
\[\text{ $f(x)$ 는 $O(g(x))$ 이다. }\]라고 한다.
이 때, \(f(x)\) 는 \(g(x)\)의 "big-oh" 라고 읽는다.
O의 증인
\(\color{red} k, \color{red} C\) 를 \(f(x)\) 가 \(O(g(x))\) 라는 관계에 대한 증인(witness)이라 부른다.
- 즉, \(f(x)\) 가 \(O(g(x))\) 라는 것을 보이기 위해서는 \(k, C\) 를 찾으면 된다.
- 만약 \(k, C\) 증인 한 쌍이 있다면, 무한히 많은 증인이 있다.
- \(C \lt C', k \lt k'\) 인 \(k', C'\) 도 증인이기 때문이다.
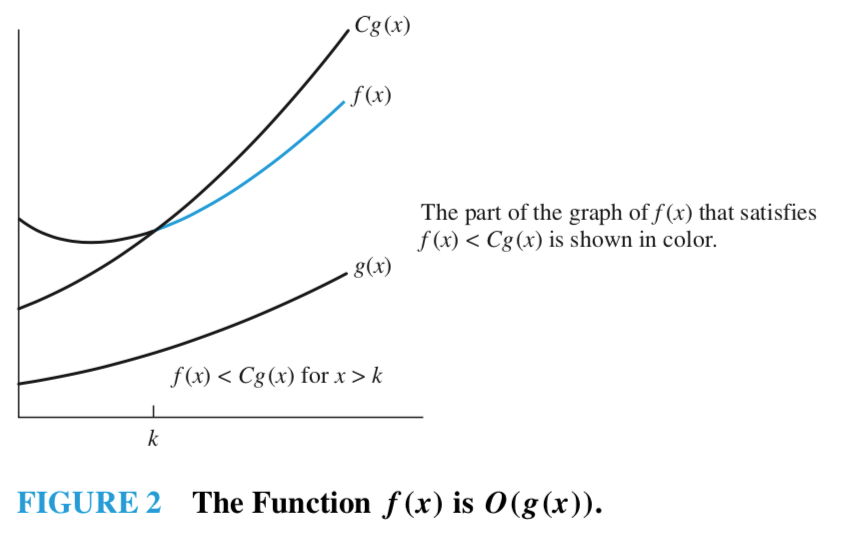
위의 그래프를 보면 쉽게 이해할 수 있다.
- \(k\) 의 최소값은 \(Cg(x) > f(x)\) 인 지점이다.
- \(C\) 의 후보는 모든 실수이기 때문에 \(Cg(x)\) 의 최고차항의 차수가 \(f(x)\) 의 최고차항의 차수보다 크거나 같다면, \(f(x)\)는 최고차항의 계수가 얼마가 되었건 \(Cg(x)\)의 증가율보다 클 수 없다.
주의: big-O 표기를 사용할 때, \(f(x)\)가 \(O(g(x))\)인 관계에 등장하는 함수 \(g\)는 가능한 한 "작은" 것을 선택하자.
big-O 예제
예제 1
\(f(x) = x^2 + 2x + 1\) 은 \(O(x^2)\) 임을 보여라.
\(x \gt \color{red}1\) 일 때 다음이 성립한다.
\[\begin{align} 0 \le x^2 + 2x + 1 & \le x^2 + 2x^2 + x^2 \\ & \le \color{red}4x^2 \\ \end{align}\]따라서 \(k = \color{red}1, C = \color{red}4\) 가 "\(f(x)\) 가 \(O(x^2)\)인 것"의 증인이 된다.
예제 2
\(7x^2\) 이 \(O(x^3)\) 임을 보여라.
일단 \(k = 7\) 로 적당한 값을 잡자.
\[\begin{align} x & \gt 7 \\ x^3 & \gt 7x^2 \\ \end{align}\]이제 \(7x^2\) 이 \(O(x^3)\) 이라 할 수 있다.
증인은 \(k = 7, C = 1\) 이다.
한편, \(x > 1\) 일 때 \(7x^2 \lt 8x^2\) 이 성립하므로 \(7x^2\) 은 \(O(x^2)\) 이기도 하다.
이 때의 증인은 \(k = 1, C = 8\) 이 된다.
From: TAOCP
TAOCP 1권의 1.2.11.1 O 표기법 챕터를 찾아보자.
Let’s look at some more examples. We know that
그럼 예들을 좀 더 보자. 다음은 우리가 알고 있는 것이다.
\[1^2 + 2^2 + ... + n^2 = \frac{1}{3}n(n + \frac{1}{2})(n+1) = \frac{1}{3}n^3 + \frac{1}{2}n^2 + \frac{1}{6}n\]so it follows that
이로부터 다음을 얻는다.
\[\begin{align} 1^2 + 2^2 + ... + n^2 & = O(n^4) & \quad (2) \\ 1^2 + 2^2 + ... + n^2 & = O(n^3) & \quad (3) \\ 1^2 + 2^2 + ... + n^2 & = \frac{1}{3}n^3 + O(n^2) & \quad (4) \\ \end{align}\]Equation (2) is rather crude, but not incorrect; Eq. (3) is a stronger statement; and Eq. (4) is stronger yet.
식 (2)가 상당히 대략적이긴 하지만, 그렇다고 부정확한 것은 아니다. 식 (3)은 좀 더 엄정한 서술이다. 그리고 식 (4)는 더욱 엄정하다.
(중략)
The O-notation is a big help in approximation work, since it describes briefly a concept that occurs often and it suppresses detailed information that is usually irrelevant. Furthermore, it can be manipulated algebraically in familiar ways, although certain important differences need to be kept in mind. The most important consideration is the idea of one-way equalities: We write \(\frac{1}{2}n^2 + n = O(n^2)\), but we never write \(O(n^2) = \frac{1}{2}n^2 + n\). (Or else, since \(\frac{1}{4}n^2 = O(n^2)\), we might come up with the absurd relation \(\frac{1}{4}n^2 = \frac{1}{2}n^2 + n\).) We always use the convention that the right-hand side of an equation does not give more information than the left-hand side; the right-hand side is a “crudification” of the left.
O 표기법은 자주 나타나는 개념을 간략히 서술하고 대체로 별 상관이 없는 세부 정보를 숨긴다는 점에서 근사를 다룰 때 큰 도움이 된다. 더 나아가서, 이 O들을 익숙한 대수적 방법으로 조작하는 것이 가능하다. 단, 몇 가지 중요한 차이들은 염두에 두어야 하는데, 가장 중요한 것이 단방향 상등(one-way equality)이라는 개념이다. 즉, \(\frac{1}{2}n^2 + n = O(n^2)\)이라고 쓸 수는 있지만 \(O(n^2) = \frac{1}{2}n^2 + n\)이라고는 절대 쓸 수 없다. (만일 그런 표기가 허용된다면, \(\frac{1}{4}n^2 = O(n^2)\)이므로 \(\frac{1}{4}n^2 = \frac{1}{2}n^2 + n\)이라는 터무니없는 결과가 나온다.) 이 표기법이 관련된 등식에서는 항상 등식의 우변이 좌변보다 더 자세한 정보를 제공하지 않는다는 관례를 사용한다. 즉, 우변은 항상 좌변보다 조악한 버전인 것이다.
Big-O 표기법에 대한 로버트 세지윅과의 문답
Q. (위 질문에 이어서) 그러면 왜 Big-O 표기법이 널리 쓰이는가?
A. 정확한 분석이 현실적으로 불가능한 복잡한 알고리즘이더라도 증가 오더의 상한을 세우는 데 도움이 된다. 그리고 Big-Omega, Big-Theta 표기법과도 호환된다. Big-Omega, Big-Theta는 컴퓨터 과학 이론 분야에서 최악 상황 성능의 상한을 구분하는 데 사용된다. 만약 \(N > N_0\)에 대해서 \(\vert f(N) \ge c \vert g(N) \vert\)을 만족하는 상수 \(c\)와 \(N_0\)가 존재하면 \(f(N)\)이 \(\Omega(g(N))\)이다, 라고 말한다. 그리고 \(f(N)\)이 \(O(g(N))\)이면서 \(\Omega(g(N))\)이기도 하다면 \(f(N)\)이 \(\Theta(g(N))\)이다, 라고 말한다. Big-Omega 표기는 최악 조건 성능 하한을 의미하고 Big-Theta 표기는 점근적인 최악 조건 성능에 있어서 그보다 더 나은 알고리즘은 존재하지 않는다는 의미로 사용한다. 즉 점근적인 성능에 있어서 최적 알고리즘임을 의미한다. 실 응용에 있어서 최적 알고리즘을 적용하는 것은 분명 최선의 선택이다. 하지만 앞으로 보게 되듯이 다른 여러 가지 고려사항들이 있다.
– 알고리즘 [개정4판]. 1.4장 206쪽.
big-Omega, Ω
Definition
Let \(f\) and \(g\) be functions from the set of integers or the set of real numbers to the set of real numbers. We say that \(f(x)\) is \(\Omega(g(x))\) if there are positive constants \(C\) and \(k\) such that
\(\vert f(x) \vert \gt C \vert g(x) \vert\)
whenever \(x \gt k\). [This is read as "\(f(x)\) is big-Omega of \(g(x)\)."] 1
함수 \(f\)와 함수 \(g\)가 정수(or 실수)의 집합으로부터 실수의 집합으로의 함수라 하자.
\(x \gt \color{red}k\) 일 때, \(\vert f(x) \vert \ge \color{red}C \vert g(x) \vert\) 를 만족하는 상수 \(C, k\) 가 존재하면,
\[\text{ $f(x)$ 는 $\Omega(g(x))$ 이다. }\]라고 한다.
이 때, \(f(x)\) 는 \(g(x)\)의 "big-Omega" 라고 읽는다.
(big-O 가 \(\vert f(x) \vert \color{blue}\le C \vert g(x) \vert\) 였음을 기억하자. 부등호 방향이 반대이다.)
예제
함수 \(f(x) = 8x^3 + 5x^2 + 7\) 은 \(\Omega (g(x))\) 이다.
여기서, \(g(x)\)는 함수 \(g(x) = x^3\) 이다.
모든 양의 실수 x에 대하여 \(f(x) = 8x^3 + 5x^2 + 7 \ge 8x^3\) 이므로 이것은 이해하기 쉽다.\(g(x) = x^3\)이 \(O(8x^3 + 5x^2 +7)\)임과 동등하다.
이것은 부등호를 반대 방향으로 돌림으로써 얻어진다. 1
big-Theta, Θ
Definition
Let \(f\) and \(g\) be functions from the set of integers or the set of real numbers to the set of real numbers. We say that \(f(x)\) is \(\Theta(g(x))\) if \(f(x)\) is \(O(g(x))\) and \(f(x)\) is \(\Omega(g(x))\). When \(f(x)\) is \(\Theta(g(x))\) we say that f is big-Theta of \(g(x)\), that \(f(x)\) is of order \(g(x)\), and that \(f(x)\) and \(g(x)\) are of the same order. 1
함수 \(f\)와 함수 \(g\)가 정수(or 실수)의 집합으로부터 실수의 집합으로의 함수라 하자.
\(f(x)\)가 \(O(g(x))\)이고, \(f(x)\)가 \(\Omega(g(x))\) 이면,
\[\text{ $f(x)$는 $\Theta(g(x))$ 이다.}\]라고 한다.
한편, \(f(x)\) 가 \(\Theta(g(x))\) 일 때 "\(f\)는 \(g(x)\)의 big-Theta" 라고 읽는다.
증가량 비교
그래프 비교
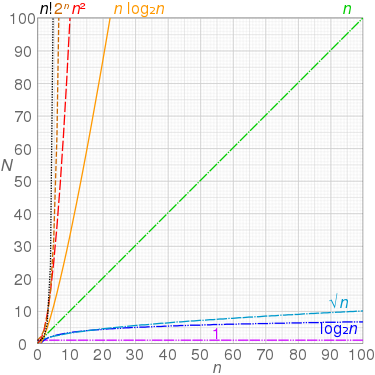
이미지 출처는 Big_O_notation(wikipedia)
주요 증가율
| 시간 복잡도 | 한국어 명칭 | 영문 명칭 | \(n\)이 두 배가 되면 |
|---|---|---|---|
| \(O(1)\) | 상수 | constant | 변함없다 |
| \(O(\log n)\) | 로그 | logarithmic | 약간의 상수만큼 커진다 |
| \(O(n)\) | 선형 | linear | 2배 커진다 |
| \(O(n \log n)\) | 선형 로그형 | linearithmic, linear logarithmic, n log n | 2배보다 약간 커진다 |
| \(O(n^2)\) | 2차형, 제곱배 | quadratic | 4배 커진다 |
| \(O(n^3)\) | 3차형 | cubic | 8배 커진다 |
| \(O(n^k)\), (상수 \(k\)) | 다항, k승배 | polynomial | \(2^k\)배 커진다 |
| \(O(k^n)\), (상수 \(k \gt 1\)) | 지수적, 기하급수배 | exponential | \(k^n\)배 커진다 |
| \(O(n!)\) | 계승 | factorial | \(n^n\)배 정도 커진다. \(n! \approx \sqrt{2 \pi n} (n / e)^n\) |
로그 \(O(\log n)\)
- 대표적인 사례
- 이진 탐색
선형 \(O(n)\)
- 대표적인 사례
- 최댓값 찾기
선형 로그형 \(O(n \log n)\)
- 로그의 밑은 증가 오더의 비교에 있어서는 의미가 없기 때문에 표기를 생략한다.2
- 대표적인 사례
- Merge sort
- Quick sort
제곱 \(O(n^2)\)
- 주로 2중 for loop를 사용하여 조합 가능한 모든 쌍을 대상으로 작업을 하는 경우가 전형적이다.
- 대표적인 사례
- Selection sort
- Insertion sort
지수(기하급수) \(O(k^n)\)
- 지수 시간 알고리즘은 몹시 느리지만, 최선의 해결책이 지수 시간 알고리즘 외에는 없는 문제군이 존재한다.
- 완전 탐색에서 지수 시간이 필요한 경우가 많다.
- 대표적인 사례
- 모든 부분집합 검사( \(2^n\) )
기본 점화식과 폐쇄형
\[\def\formularaa{ T(n) = \begin{cases} \Theta(1), & n = 1 \\ T(n-1) + \Theta(1), & n \ge 2 \\ \end{cases} } \def\formularbb{ T(n) = \begin{cases} \Theta(1), & n = 1 \\ T(n-1) + \Theta(n), & n \ge 2 \\ \end{cases} } \def\formularcc{ T(n) = \begin{cases} \Theta(1), & n = 1 \\ T(\frac{n}{2}) + \Theta(1), & n \ge 2 \\ \end{cases} } \def\formulardd{ T(n) = \begin{cases} \Theta(1), & n = 1 \\ T(\frac{n}{2}) + \Theta(n), & n \ge 2 \\ \end{cases} } \def\formularee{ T(n) = \begin{cases} \Theta(1), & n = 1 \\ 2 T(\frac{n}{2}) + \Theta(1), & n \ge 2 \\ \end{cases} } \def\formularff{ T(n) = \begin{cases} \Theta(1), & n = 1 \\ 2T(\frac{n}{2}) + \Theta(n), & n \ge 2 \\ \end{cases} }\]다음 표는 [LEE] 1.6장을 인용한 것이다.
| 점화식 | 폐쇄형 | 비고 |
|---|---|---|
| \(\formularaa\) | \(T(n) = \Theta(n)\) | |
| \(\formularbb\) | \(T(n) = \Theta(n^2)\) | [[/algorithm/quick-sort]]의 최악의 수행 시간 |
| \(\formularcc\) | \(T(n) = \Theta(\log n)\) | 이진 탐색의 수행 시간 |
| \(\formulardd\) | \(T(n) = \Theta(n)\) | |
| \(\formularee\) | \(T(n) = \Theta(n)\) | |
| \(\formularff\) | \(T(n) = \Theta(n \log n)\) | [[/algorithm/merge-sort]]의 수행 시간, [[/algorithm/quick-sort]]의 최선의 수행 시간 |
예제로 이해하자
쉬운 예제
상수항은 무시하고, 지배적이지 않은 항도 무시한다.
| 식 | 상한 |
|---|---|
| \(f(n) = 5n + 3\) | \(O(n)\) |
| \(f(n) = 3n^2 - 3\) | \(O(n^2)\) |
| \(f(n) = 5n^3 - n^2\) | \(O(n^3)\) |
| \(O(n^2 + n)\) | \(O(n^2)\) |
| \(O(n + \log n)\) | \(O(n)\) |
| \(O(5 \times 2^n + 1000 \times n^{100})\) | \(O(2^n)\) |
| \(O(n + m)\) | \(O(n + m)\) |
이중 루프
function test(list) {
for (var i = 0; i < list.length; i++) {
for (var j = 0; j < list.length; j++) {
console.log(i + ',' + j);
}
}
}
list의 길이를 n이라 하면, list를 이중으로 돌리고 있으므로 \(O(n^2)\) 이다.
안쪽 루프가 1씩 줄어드는 이중 루프
아래의 코드는 j가 i+1로 시작하므로 루프가 진행될수록 안쪽 루프의 횟수가 줄어든다.
좀 헷갈린다.
function test(list) {
for (var i = 0; i < list.length; i++) {
// j = i + 1 에 주목
for (var j = i + 1; j < list.length; j++) {
console.log(i + ',' + j);
}
}
}
그러나 반복 횟수를 다음과 같이 생각해 보면 \(O(\frac{1}{2}n^2) = O(n^2)\) 임을 알 수 있다.
\[\begin{align} & (n-1) + (n-2) + (n-3) + ... + 2 + 1 \\ & = \sum_1^{n-1} k = \frac{(n-1)n}{2} = \frac{n^2 - n}{2}\\ & = \frac{1}{2}n^2 - \frac{1}{2}n \\ & \therefore O(n^2) \\ \end{align}\]두 개의 다른 리스트를 루프하는 이중 루프
function test(listA, listB) {
// 바깥쪽 루프는 listA
for (var i = 0; i < listA.length; i++) {
// 안쪽 루프는 listB
for (var j = 0; j < listB.length; j++) {
console.log(i + ',' + j);
}
}
}
listA의 길이를 a, listB의 길이를 b라 하자.
- 답은 \(O(a \cdot b)\).
- 느낌상 \(O(n^2)\)일 것 같지만, 아니다.
- 두 리스트의 길이가 같으리란 보장이 없다.
- 두 리스트의 크기를 모두 고려해야 한다.
그렇다면 아래와 같은 삼중 루프는 어떻게 될까?
function test(listA, listB) {
for (var i = 0; i < listA.length; i++) {
for (var j = 0; j < listB.length; j++) {
for (var k = 0; k < 99999; k++) {
console.log(i + ',' + j + ',' + k);
}
}
}
}
- 답은 \(O(a \cdot b \cdot 99999) = O(a \cdot b)\).
99999는 상수이므로 무시한다.
문자열 배열 정렬 문제
이 문제의 출처는 코딩 인터뷰 완전 분석이다.
다음과 같은 알고리즘이 있다고 하자.
- 여러 개의 문자열로 구성된 배열(
String[])이 주어진다. - 각각의 문자열을 먼저
abc순으로 정렬한다. - 배열(
String[])을 정렬한다.
알고리즘의 수행 시간은?
- 이 문제는 생각보다 까다롭다.
- 얼핏 생각해보면 \(O(n \cdot n \log n + n \log n) = O(n^2 \log n)\)일 것 같지만 틀린 답이다.
제대로 풀어보면 다음과 같다.
- 정의
- 가장 길이가 긴 문자열의 길이를
s라 하자. - 배열의 길이를
a라 하자.
- 가장 길이가 긴 문자열의 길이를
- 문자열 정렬
- 문자열 하나하나를 정렬하는데 \(O(s \cdot \log s)\) 소요.
- 문자열은 모두
a개. - 즉, 모든 문자열 정렬에 \(O(a \cdot s \cdot \log s)\) 소요.
- 배열 정렬
- 배열의 길이 :
a - 문자열 두 개를 비교(최악의 경우) : \(O(s)\)
- 정렬에 필요한 시간 : \(O(a \cdot \log a)\)
- 즉, 배열을 정렬하는 데에 \(O(s \cdot a \cdot \log a)\) 소요.
- 배열의 길이 :
- 결론
- \(O(a \cdot s \cdot \log s + s \cdot a \cdot \log a) = O\biggr(a \cdot s (\log s + \log a)\biggr)\).
- 이보다 더 줄일 수는 없다.
함께 읽기
- [[/algorithm/average-complexity]]{평균 계산 복잡도 구하기}
- [[master-theorem]]{마스터 정리}
- [[tilde-approximations]]{틸다 표기법}
참고문헌
- [CLRS] Introduction to Algorithms 3판 / 토머스 코멘, 찰스 레이서손, 로날드 리베스트, 클리포드 스타인 공저 / 문병로, 심규석, 이충세 공역 / 한빛아카데미 / 2014년 06월 30일
- [ROSEN] Rosen의 이산수학 / Kenneth H. Rosen 저 / 공은배 등저 / 한국맥그로힐(McGraw-Hill KOREA) / 2017년 01월 06일
- [TAOCP] The art of computer programming 1 기초 알고리즘(개정3판) / 도널드 커누스 저 / 한빛미디어 / 2006년 09월 18일
- [NAR] 다양한 예제로 학습하는 데이터 구조와 알고리즘 for Java / 나라심하 카루만치 저 / 전계도, 전형일 공역 / 인사이트(insight) / 2014년 02월 22일
- [SED] 알고리즘 [개정4판] / 로버트 세지윅, 케빈 웨인 저/권오인 역 / 길벗 / 초판 2018년 12월 26일
- [COM] 컴퓨터과학이 여는 세계 / 이광근 저 / 인사이트(insight) / 2017년 02월 28일
- [COD] 코딩인터뷰 완전분석 187가지 프로그래밍 문제와 해법 [개정판] / 게일 라크만 맥도웰 저 / 이창현 역 / 인사이트(insight) / 2017년 08월 14일
-
[LEE] 알고리즘 / 이관용, 김진욱 공저 / 한국방송통신대학교출판문화원 / 2018년 01월 25일
- Big_O_notation(wikipedia)