구체수학 02.합.05.일반적인 방법들

개요
방법 0: 답을 찾아본다
방법 1: 답을 추측하고 귀납법으로 증명한다
방법 2: 합을 어지럽힌다(섭동)
방법 3: 레퍼토리를 구축한다
- 일반식 만들기
- 문제를 해결하기
방법 4: 합을 적분으로 대체한다
- 곡선 위쪽의 넓이를 구하자
- 곡선 위쪽의 넓이를 적분으로 구하자
그 외의 방법들 (방법 6, 7)
Links

이 문서는 (책) CONCRETE MATHEMATICS(구체수학) 2장.합 - 5.일반적인 방법들을 공부한 노트입니다.

개요

이번 장의 목표는 한 가지 문제를 다양한 방법으로 풀어보며 배운 바를 정리하는 것이다.

그리고 그 문제는 0부터 n까지의 거듭제곱의 합이다.

◻_{n} = \sum_{0 \leq k \leq n} k^{2}, f o r n \geq 0.

$\Box_n = \sum_{0 \le k \le n} k^2, \quad for \; n \ge 0.$

위의 합 식은 python 코드로 생각하자면 다음과 같다.

def box(n):
    sum = 0
    for k in range(n+1):
        sum += k**2
    return sum

앞으로 쭉 참고하게 될 것이므로 0~12 사이의 n과 n^2, Box(n) 값을 다음과 같이 구하였다.

for n in range(12 + 1):
    print(n, n**2, box(n))

결과를 다음과 같이 표로 정리해 보았다.
- 가장 오른쪽 열은 표를 정리하다가, 점화식 구조를 떠올리게 되어 추가한 것이다.

$n$	$n^2$	$\Box_n$	$\Box_n = n^2 + \Box_{n-1}$
0	0	0	0
1	1	1	= 1 + 0
2	4	5	= 4 + 1
3	9	14	= 9 + 5
4	16	30	= 16 + 14
5	25	55	= 25 + 30
6	36	91	= 36 + 55
7	49	140	= 49 + 91
8	64	204	= 64 + 140
9	81	285	= 81 + 204
10	100	385	= 100 + 285
11	121	506	= 121 + 385
12	144	650	= 144 + 506

방법 0: 답을 찾아본다

Method 0: You could look it up.

이런 문제는 아마도 옛날 사람들이 다 풀어 놨을 것이다.

따라서 책이나 인터넷에서 답을 찾아본다.

교재에서는 CRC Standard Mathematical Tables에서 답을 찾았다고 한다.
나는 그냥 Wolfram Alpha에서 찾았다.
- https://www.wolframalpha.com/input/?i=sum+0+to+n+k%5E2

이 문제의 닫힌 형식은 다음과 같다. 고등학교에서 배웠던 익숙한 공식이다.

\begin{matrix} (2.38) & ◻_{n} = \frac{n (n + 1) (2 n + 1)}{6}, f o r n \geq 0. \end{matrix}

$\Box_n = { n(n+1)(2n+1) \over 6 }, \quad for \; n \ge 0. \tag{2.38} \label{2.38}$

이 식을 python으로 옮기면 다음과 같을 것이다. 최적화되어 시간 복잡도가 선형 시간에서 상수 시간이 된 것 같다.

def Box(n):
    return n * (n+1) * (2*n+1) / 6

한편, 식을 전개하면 $\Box_n = { 2n^3 + 3n^2 + n \over 6 }$ 이 되므로 다음과 같이 표현하는 것도 가능하다.

def Box(n):
    return (2*(n**3) + 3*(n**2) + n) / 6

방법 1: 답을 추측하고 귀납법으로 증명한다

Method 1: Guess the answer, prove it by induction.

일단 위에서 얻은 답은 잊어버리자.

그리고 이 책을 읽고 있는 내가 열심히 생각해서 다음과 같은 답을 추측했다고 치자.

◻_{n} = \frac{n (n + \frac{1}{2}) (n + 1)}{3}, f o r n \geq 0.

$\Box_n = { n(n+\frac{1}{2})(n+1) \over 3 }, \quad for \; n \ge 0.$

여기에서 중요한 것은 열심히 생각해서 떠올려 추측하는 것.
별 생각이 안 난다면 이 방법은 사용할 수 없다.
주관식 답을 찍는 것과 비슷하다. 그러나 그것보다는 조금 더 열심히 생각해야 한다.

이 답이 맞을 수도 있고, 틀릴 수도 있다.

그러니 수학적 귀납법으로 맞는지를 확인하면 된다.

수학적 귀납법으로 위의 추측을 검증하는 방법은 다음과 같다.

점화식을 준비한다.
점화식에 추측한 답을 대입해 모순이 없는지를 확인하면 된다.

그렇다면 주어진 문제를 통해 점화식을 만들어 보자.

재귀 함수를 만드는 과정과 똑같다.
재귀가 멈추는 조건인 n = 0일 때부터 만들자.

◻_{0} = 0^{2} = 0

$\Box_0 = 0^2 = 0$

이제 $\Box_n$ 과 $\Box_{n-1}$ 의 관계를 찾아주면 된다.

\begin{aligned} ◻_{n} & = \sum_{0 \leq k \leq n} k^{2}, f o r n \geq 0. \\ = 0^{2} + 1^{2} + 2^{2} + . . . + (n - 1)^{2} + n^{2} \\ = (0^{2} + 1^{2} + 2^{2} + . . . + (n - 1)^{2}) + n^{2} \\ = (◻_{n - 1}) + n^{2} \end{aligned}

$\begin{align} \Box_n & = \sum_{0 \le k \le n} k^2, \quad for \; n \ge 0. \\ & = 0^2 + 1^2 + 2^2 + ... + (n-1)^2 + n^2 \\ & = \left( 0^2 + 1^2 + 2^2 + ... + (n-1)^2 \right) + n^2 \\ & = \left( \Box_{n-1} \right) + n^2 \\ \end{align}$

따라서 점화식은 다음과 같이 꾸밀 수 있을 것이다.

\begin{aligned} ◻_{0} & = 0; \\ ◻_{n} & = ◻_{n - 1} + n^{2}, f o r n \leq 0. \end{aligned}

$\begin{align} \Box_0 & = 0; \\ \Box_n & = \Box_{n-1} + n^2, \quad for \; n \le 0. \\ \end{align}$

def box(n):
    if n == 0:
        return 0
    return Box(n-1) + n**2

이제 점화식에 추측한 식을 넣어보고, 모순이 없는지를 확인하면 된다.

\begin{aligned} ◻_{n} & = ◻_{n - 1} + n^{2} \\ (\frac{n (n + \frac{1}{2}) (n + 1)}{3}) & = (\frac{(n - 1) (n - 1 + \frac{1}{2}) (n - 1 + 1)}{3}) + n^{2} \\ 양 변에 3을 곱하자 \\ n (n + \frac{1}{2}) (n + 1) & = (n - 1) (n - 1 + \frac{1}{2}) (n - 1 + 1) + 3 n^{2} \\ n (n + \frac{1}{2}) (n + 1) & = (n - 1) (n - \frac{1}{2}) n + 3 n^{2} \\ 양 변을 n으로 나누자 \\ (n + \frac{1}{2}) (n + 1) & = (n - 1) (n - \frac{1}{2}) + 3 n \\ n^{2} + \frac{3}{2} \cdot n + \frac{1}{2} & = (n - 1) (n - \frac{1}{2}) + 3 n \\ n^{2} + \frac{3}{2} \cdot n + \frac{1}{2} & = n^{2} - \frac{3}{2} \cdot n + \frac{1}{2} + 3 n \\ \frac{3}{2} \cdot n & = - \frac{3}{2} \cdot n + 3 n \\ \frac{6}{2} \cdot n & = 3 n \\ 3 n & = 3 n \end{aligned}

$\require{cancel} \begin{align} \Box_n & = \Box_{n-1} + n^2 \\ \\ \left( { n(n+\frac{1}{2})(n+1) \over 3 } \right) & = \left( { (n-1)(n - 1+\frac{1}{2})(n - 1 +1) \over 3 } \right) + n^2 \\ & \color{gray}{\text{양 변에 3을 곱하자}}\\ n(n+\frac{1}{2})(n+1) & = (n-1)(n - 1+\frac{1}{2})(n - 1 +1) + 3n^2 \\ n(n+\frac{1}{2})(n+1) & = (n-1)(n - \frac{1}{2})n + 3n^2 \\ & \color{gray}{\text{양 변을 n으로 나누자}}\\ (n+\frac{1}{2})(n+1) & = (n-1)(n - \frac{1}{2}) + 3n \\ n^2 + \frac{3}{2} \cdot n + \frac{1}{2} & = (n-1)(n - \frac{1}{2}) + 3n \\ \cancel{n^2} + \frac{3}{2} \cdot n + \cancel{\frac{1}{2}} & = \cancel{n^2} - \frac{3}{2} \cdot n + \cancel{\frac{1}{2}} + 3n \\ \frac{3}{2} \cdot n & = - \frac{3}{2} \cdot n + 3n \\ \frac{6}{2} \cdot n & = 3n \\ 3n & = 3n \\ \end{align}$

따라서 추측이 맞다고 볼 수 있다.

그리고 추측한 값은, 다음과 같이 변형해보면 방법 0에서 알아낸 식과 똑같다.

\begin{aligned} ◻_{n} & = \frac{n (n + \frac{1}{2}) (n + 1)}{3} \\ = \frac{n \cdot 2 \cdot (n + \frac{1}{2}) (n + 1)}{2 \cdot 3} \\ = \frac{n (2 n + 1) (n + 1)}{6} \\ = \frac{n (n + 1) (2 n + 1)}{6} \end{aligned}

$\begin{align} \Box_n & = { n(n+\frac{1}{2})(n+1) \over 3 } \\ & = { n \cdot 2 \cdot (n+\frac{1}{2})(n+1) \over 2 \cdot 3 } \\ & = { n (2n+1)(n+1) \over 6 } \\ & = { n (n+1)(2n+1) \over 6 } \\ \end{align}$

닫힌 형식을 구했다!

방법 2: 합을 어지럽힌다(섭동)

Method 2: Perturb the sum.

섭동법은 다음과 같은 방법이다.

합 $S_{n + 1}$ 을 다음 두 가지 방법으로 표현한다.
- 첫번째: 합의 마지막 항을 뽑아낸다.
  - 예: $S_{n+1} = S_n + a_{n+1}$
- 두번째: 합의 첫 항을 뽑아낸다.
  - 예: $S_{n+1} = a_0 + \sum_{1 \le k \le n+1} a_k = a_0 + \sum_{0 \le k \le n} a_{k+1}$
첫번째 식과 두번째 식을 같다고 놓고, 적절히 조작해서 $S_n$ 으로 표현한다.

섭동법을 적용해보자.

첫번째: 합의 마지막 항을 뽑아낸다.

◻_{n + 1} = ◻_{n} + (n + 1)^{2}

$\Box_{n+1} = \Box_n + (n+1)^2$

두번째: 합의 첫 항을 뽑아낸다.

\begin{aligned} ◻_{n + 1} & = 0^{2} + \sum_{1 \leq k \leq n + 1} k^{2} \\ = 0^{2} + \sum_{0 \leq k \leq n} (k + 1)^{2} \end{aligned}

$\begin{align} \Box_{n+1} & = 0^2 + \sum_{1 \le k \le n+1} k^2 \\ & = 0^2 + \sum_{0 \le k \le n} (k+1)^2 \\ \end{align}$

이제 둘을 조합한다.

\begin{aligned} ◻_{n} + (n + 1)^{2} & = 0^{2} + \sum_{0 \leq k \leq n} (k + 1)^{2} \\ = \sum_{0 \leq k \leq n} (k^{2} + 2 k + 1) \\ = \sum_{0 \leq k \leq n} k^{2} + \sum_{0 \leq k \leq n} 2 k + \sum_{0 \leq k \leq n} 1 \\ = ◻_{n} + \sum_{0 \leq k \leq n} 2 k + \sum_{0 \leq k \leq n} 1 \\ = ◻_{n} + 2 \sum_{0 \leq k \leq n} k + (n + 1) \\ = ◻_{n} + 2 \cdot \frac{n (n + 1)}{2} + (n + 1) \\ = ◻_{n} + n (n + 1) + (n + 1) \\ ◻_{n} + (n + 1)^{2} & = ◻_{n} + n^{2} + 2 n + 1 \end{aligned}

$\begin{align} \Box_n + (n+1)^2 & = 0^2 + \sum_{0 \le k \le n} (k+1)^2 \\ & = \sum_{0 \le k \le n} (k^2 + 2k + 1) \\ & = \sum_{0 \le k \le n} k^2 + \sum_{0 \le k \le n} 2k + \sum_{0 \le k \le n} 1 \\ & = \Box_n + \sum_{0 \le k \le n} 2k + \sum_{0 \le k \le n} 1 \\ & = \Box_n + 2 \sum_{0 \le k \le n} k + (n + 1) \\ & = \Box_n + 2 \cdot \frac{n(n+1)}{2} + (n + 1) \\ & = \Box_n + n(n+1) + (n + 1) \\ \\ \Box_n + (n+1)^2 & = \Box_n + n^2 + 2n + 1 \\ \end{align}$

0 = 0 모양이 나와 작업이 실패하였다.

그렇다면 조금 더 머리를 굴려서 $\sum k^2$ 모양이 남도록 조작을 할 궁리를 해야 한다.

방금 양 변이 $\sum k^2 ... = \sum k^2 ...$ 의 모양이 되어 $\Box_n$ 이 소거되었는데, 혹시 $\sum k^3$ 을 사용하면 양 변이 $\sum k^3 ... = \sum k^3 ...$ 이 되고 $\sum k^2$ 가 남을 가능성은 없을까? 궁금하니 시도해 보자.

일단 다음과 같이 세제곱의 합을 정의하자.

{�x2750;}_{n} = \sum_{0 \leq k \leq n} k^{3}

$\unicode{0x2750}_n = \sum_{0 \le k \le n} k^3$

그렇다면 다음과 같이 섭동법을 적용해 보자.

첫번째: 합의 마지막 항을 뽑아낸다.

{�x2750;}_{n + 1} = {�x2750;}_{n} + (n + 1)^{3}

$\unicode{0x2750}_{n+1} = \unicode{0x2750}_n + (n+1)^3$

두번째: 합의 첫 항을 뽑아낸다.

{�x2750;}_{n + 1} = 0^{3} + \sum_{0 \leq k \leq n} (k + 1)^{3}

$\unicode{0x2750}_{n+1} = 0^3 + \sum_{0 \le k \le n} (k+1)^3$

이제 둘을 조합한다.

\begin{aligned} {�x2750;}_{n} + (n + 1)^{3} & = 0^{3} + \sum_{0 \leq k \leq n} (k + 1)^{3} \\ = \sum_{0 \leq k \leq n} (k^{3} + 3 k^{2} + 3 k + 1) \\ = \sum_{0 \leq k \leq n} k^{3} + \sum_{0 \leq k \leq n} 3 k^{2} + \sum_{0 \leq k \leq n} 3 k + \sum_{0 \leq k \leq n} 1 \\ = {�x2750;}_{n} + \sum_{0 \leq k \leq n} 3 k^{2} + \sum_{0 \leq k \leq n} 3 k + \sum_{0 \leq k \leq n} 1 \\ (n + 1)^{3} & = \sum_{0 \leq k \leq n} 3 k^{2} + \sum_{0 \leq k \leq n} 3 k + \sum_{0 \leq k \leq n} 1 \\ (n + 1)^{3} & = 3 ◻_{n} + \sum_{0 \leq k \leq n} 3 k + \sum_{0 \leq k \leq n} 1 \\ n^{3} + 3 n^{2} + 3 n + 1 & = 3 ◻_{n} + 3 \cdot \frac{n (n + 1)}{2} + (n + 1) \\ 2 n^{3} + 6 n^{2} + 6 n + 2 & = 6 ◻_{n} + 3 n (n + 1) + 2 (n + 1) \\ 2 n^{3} + 6 n^{2} + 6 n + 2 & = 6 ◻_{n} + 3 n^{2} + 5 n + 2 \\ 2 n^{3} + 3 n^{2} + n & = 6 ◻_{n} \\ ◻_{n} & = \frac{2 n^{3} + 3 n^{2} + n}{6} \\ = \frac{n (2 n^{2} + 3 n + 1)}{6} \\ = \frac{n (n + 1) (2 n + 1)}{6} \end{aligned}

$\begin{align} \unicode{0x2750}_n + (n+1)^3 & = 0^3 + \sum_{0 \le k \le n} (k+1)^3 \\ & = \sum_{0 \le k \le n} (k^3 + 3k^2 + 3k +1) \\ & = \sum_{0 \le k \le n} k^3 + \sum_{0 \le k \le n}3k^2 + \sum_{0 \le k \le n}3k + \sum_{0 \le k \le n}1 \\ & = \unicode{0x2750}_n + \sum_{0 \le k \le n}3k^2 + \sum_{0 \le k \le n}3k + \sum_{0 \le k \le n}1 \\ (n+1)^3 & = \sum_{0 \le k \le n}3k^2 + \sum_{0 \le k \le n}3k + \sum_{0 \le k \le n}1 \\ (n+1)^3 & = 3 \Box_n + \sum_{0 \le k \le n}3k + \sum_{0 \le k \le n}1 \\ n^3 + 3n^2 + 3n + 1 & = 3 \Box_n + 3 \cdot \frac{n(n+1)}{2} + (n+1) \\ 2n^3 + 6n^2 + 6n + 2 & = 6 \Box_n + 3 n(n+1) + 2(n+1) \\ 2n^3 + 6n^2 + 6n + 2 & = 6 \Box_n + 3n^2 + 5n + 2 \\ 2n^3 + 3n^2 + n & = 6 \Box_n \\ \Box_n & = { 2n^3 + 3n^2 + n \over 6 } \\ & = { n(2n^2 + 3n + 1) \over 6 } \\ & = { n(n + 1)(2n + 1) \over 6 } \\ \end{align}$

닫힌 형식을 구했다!

방법 3: 레퍼토리를 구축한다

Build a repertoire.

일단 점화식은 다음과 같다.

\begin{aligned} ◻_{0} & = 0; \\ ◻_{n} & = ◻_{n - 1} + n^{2}, f o r n \leq 0. \end{aligned}

$\begin{align} \Box_0 & = 0; \\ \Box_n & = \Box_{n-1} + n^2, \quad for \; n \le 0. \\ \end{align}$

레퍼토리법을 적용하려면 이를 일반화해야 한다.

그 다음, 일반식에 위의 점화식을 적용하여 답을 구하면 된다.

일반식 만들기

$n^2$ 을 사용하는 점화식이므로 일반식은 다음과 같다.

\begin{aligned} R_{0} & = α; \\ R_{n} & = R_{n - 1} + β + γ n + δ n^{2}, f o r n \leq 0. \end{aligned}

$\begin{align} R_0 & = \alpha; \\ R_n & = R_{n-1} + \beta + \gamma n + \delta n^2, \quad for \; n \le 0. \\ \end{align}$

그리고 닫힌 형태의 해가 다음과 같다고 하자.

R_{n} = A (n) α + B (n) β + C (n) γ + D (n) δ

$R_n = A(n) \alpha + B(n) \beta + C(n) \gamma + D(n) \delta$

$\alpha$ 는 초항이고, 항을 거듭해가며 더해도 딱 한 번만 더해지므로 $A(n) = 1$ 이다.
$\beta$ 는 항을 거듭해가며 더해가는 상수이므로 $B(n) = n$ 이다.
$\gamma$ 는 항을 거듭해가며 n을 몇 번 더해가는지이므로 $C(n) = \frac{n(n+1)}{2}$ 이다.
$δ$ 는 항을 거듭해가며 n^2을 몇 번 더해가는지… 인데 아직 모른다.
- $D(n)$ 만 구하면 되겠다.

참고: 1, 2, 3 항목이 잘 이해가지 않으면 02.합.02.합과 점화식 문서를 다시 읽고 레퍼토리법을 복습하자.

$\alpha, \beta, \gamma$ 는 쉽게 구했지만 $\delta$ 는 아직 구하지 못했다.

$R_n = n^3$ 이라면

\begin{aligned} R_{0} & = A (0) α + B (0) β + C (0) γ + D (0) γ \\ = α = 0^{3} \\ ∴ α = 0 \\ R_{1} & = A (1) α + B (1) β + C (1) γ + D (1) γ \\ = α + β + γ \cdot 1 + δ \cdot 1^{2} = 1^{3} \\ = α + β + γ + δ = 1 \\ = β + γ + δ = 1 \\ R_{2} & = A (2) α + B (2) β + C (2) γ + D (2) γ \\ = α + β \cdot 2 + γ \cdot (1 + 2) + δ \cdot (1^{2} + 2^{2}) = 2^{3} \\ = 2 β + 3 γ + 5 δ = 8 \\ R_{3} & = A (3) α + B (3) β + C (3) γ + D (3) γ \\ = α + β \cdot 3 + γ \cdot (1 + 2 + 3) + δ \cdot (1^{2} + 2^{2} + 3^{2}) = 3^{3} \\ = 3 β + 6 γ + 14 δ = 27 \end{aligned}

$\begin{align} R_0 & = A(0) \alpha + B(0) \beta + C(0) \gamma + D(0) \gamma \\ & = \color{red}{\alpha = 0^3} \\ & \therefore \alpha = 0 \\ \\ R_1 & = A(1) \alpha + B(1) \beta + C(1) \gamma + D(1) \gamma \\ & = \alpha + \beta + \gamma \cdot 1 + \delta \cdot 1^2 = 1^3 \\ & = \alpha + \beta + \gamma + \delta = 1 \\ & = \color{red}{\beta + \gamma + \delta = 1} \\ \\ R_2 & = A(2) \alpha + B(2) \beta + C(2) \gamma + D(2) \gamma \\ & = \alpha + \beta \cdot 2 + \gamma \cdot (1+2) + \delta \cdot (1^2 + 2^2) = 2^3 \\ & = \color{red}{2 \beta + 3 \gamma + 5 \delta = 8} \\ \\ R_3 & = A(3) \alpha + B(3) \beta + C(3) \gamma + D(3) \gamma \\ & = \alpha + \beta \cdot 3 + \gamma \cdot (1+2+3) + \delta \cdot (1^2 + 2^2 + 3^2) = 3^3 \\ & = \color{red}{3 \beta + 6 \gamma + 14 \delta = 27} \\ \end{align}$

변수가 셋, 식이 셋이니 이제 연립 방정식을 풀 수 있다.

{\begin{cases} β + γ + δ & = 1 \\ 2 β + 3 γ + 5 δ & = 8 \\ 3 β + 6 γ + 14 δ & = 27 \end{cases}

$\begin{cases} \beta + \gamma + \delta & = 1 \\ 2\beta + 3\gamma + 5\delta & = 8 \\ 3\beta + 6\gamma + 14\delta & = 27 \\ \end{cases}$

$\beta + \gamma + \delta = 1$ 를 써서 나머지 두 식을 심플하게 바꿔보자.

{\begin{cases} β + γ + δ & = 1 & . . . (가) \\ 2 β + 3 γ + 5 δ & = 8 & . . . (나) \\ 3 β + 6 γ + 14 δ & = 27 & . . . (다) \end{cases} 식 하나를 소거하자. {\begin{cases} - β + 2 δ & = 5 & . . . (나 - 3 가) \\ - 3 β + 8 δ & = 21 & . . . (다 - 6 가) \end{cases} 이제 변수 하나의 값을 구할 수 있다. \begin{array}{cccc} - 3 β & + 6 δ & = 15 \\ - & - 3 β & + 8 δ & = 21 \\ - 2 δ & = - 6 \end{array} \begin{array}{lll} ∴ δ & = 3 \\ ∴ β & = 1 & ∵ - β + 2 δ = 5 \\ ∴ γ & = - 3 & ∵ β + γ + δ = 1 \end{array}

$\begin{cases} \beta + \gamma + \delta & = 1 & ... (가) \\ 2\beta + 3\gamma + 5\delta & = 8 & ... (나) \\ 3\beta + 6\gamma + 14\delta & = 27 & ... (다) \\ \end{cases} \\ \color{gray}{\text{식 하나를 소거하자.}} \\ \begin{cases} - \beta + 2 \delta & = 5 & ... (나 - 3가) \\ - 3\beta + 8\delta & = 21 & ... (다 - 6가) \\ \end{cases} \\ \color{gray}{\text{이제 변수 하나의 값을 구할 수 있다.}} \\ \begin{array}{c|ccc} & - 3\beta & + 6 \delta & = 15 \\ - & - 3\beta & + 8 \delta & = 21 \\ \hline & & - 2 \delta & = -6 \\ \end{array} \\ \\ \begin{array}{lll} \therefore \delta & = 3 \\ \therefore \beta & = 1 & \because -\beta + 2\delta = 5\\ \therefore \gamma & = -3 & \because \beta + \gamma + \delta = 1\\ \end{array}$

이제 $D(n)$ 을 구하기 위해 다음과 같이 식을 꾸밀 수 있다.

\begin{aligned} R_{n} & = A (n) α + B (n) β + C (n) γ + D (n) δ \\ n^{3} & = A (n) \cdot 0 + B (n) \cdot 1 + C (n) \cdot (- 3) + D (n) \cdot 3 \\ = B (n) - 3 C (n) + 3 D (n) \\ 3 D (n) & = n^{3} - B (n) + 3 C (n) \\ = n^{3} - n + 3 \cdot \frac{n (n + 1)}{2} \\ 6 D (n) & = 2 n^{3} - 2 n + 3 n (n + 1) \\ = 2 n^{3} - 2 n + 3 n^{2} + 3 n \\ = 2 n^{3} + 3 n^{2} + n \\ D (n) & = \frac{2 n^{3} + 3 n^{2} + n}{6} \\ = \frac{n (2 n^{2} + 3 n + 1)}{6} \\ = \frac{n (n + 1) (2 n + 1)}{6} \end{aligned}

$\begin{align} R_n & = A(n) \alpha + B(n) \beta + C(n) \gamma + D(n) \delta \\ \\ n^3 & = A(n) \cdot 0 + B(n) \cdot 1 + C(n) \cdot (-3) + D(n) \cdot 3 \\ & = B(n) -3 C(n) + 3 D(n) \\ \\ 3 D(n) & = n^3 - B(n) + 3 C(n) \\ & = n^3 - n + 3 \cdot \frac{n(n+1)}{2} \\ 6 D(n) & = 2 n^3 - 2n + 3 n(n+1) \\ & = 2 n^3 - 2n + 3n^2 + 3n \\ & = 2 n^3 + 3n^2 + n \\ D(n) & = { 2 n^3 + 3n^2 + n \over 6 } \\ & = { n(2 n^2 + 3n + 1) \over 6 } \\ & = { n(n+1)(2n+1) \over 6 } \\ \end{align}$

이제 D(n)까지 다 구했다.

따라서 $\Box_n = D(n)$ 이 된다.

문제를 해결하기

일반식은 다음과 같다.

R_{n} = A (n) α + B (n) β + C (n) γ + D (n) δ

$R_n = A(n) \alpha + B(n) \beta + C(n) \gamma + D(n) \delta$

그리고 A(n), B(n), C(n), D(n)는 다음과 같다.

{\begin{cases} A (n) & = 1 \\ B (n) & = n \\ C (n) & = \sum_{k = 0}^{n} k = \frac{n (n + 1)}{2} \\ D (n) & = \sum_{k = 0}^{n} k^{2} = \frac{n (n + 1) (2 n + 1)}{6} \end{cases}

$\begin{cases} A(n) & = 1 \\ B(n) & = n \\ C(n) & = \sum_{k=0}^n k = \frac{n(n+1)}{2} \\ D(n) & = \sum_{k=0}^n k^2 = { n(n+1)(2n+1) \over 6 } \\ \end{cases}$

그리고 일반화한 점화식은 다음과 같다.

\begin{aligned} R_{0} & = α; \\ R_{n} & = R_{n - 1} + β + γ n + δ n^{2}, f o r n \leq 0. \end{aligned}

$\begin{align} R_0 & = \alpha; \\ R_n & = R_{n-1} + \beta + \gamma n + \delta n^2, \quad for \; n \le 0. \\ \end{align}$

마지막으로 해결해야 하는 점화식은 다음과 같았다!

\begin{aligned} ◻_{0} & = 0; \\ ◻_{n} & = ◻_{n - 1} + n^{2}, f o r n \leq 0. \end{aligned}

$\begin{align} \Box_0 & = 0; \\ \Box_n & = \Box_{n-1} + n^2, \quad for \; n \le 0. \\ \end{align}$

일반 점화식과 비교해 보자.

\begin{aligned} R_{n} = & R_{n - 1} + β + γ n + δ n^{2} \\ ◻_{n} = & ◻_{n - 1} + n^{2} \end{aligned}

$\begin{align} R_n = & R_{n-1} + \beta + \gamma n + \delta n^2 \\ \Box_n = & \Box_{n-1} + n^2 \\ \end{align}$

모양이 심플해서 각 변수를 다음과 같이 설정하면, $R_n = \Box_n$ 이 된다는 것을 알 수 있다.

{\begin{cases} α & = 0 \\ β & = 0 \\ γ & = 0 \\ δ & = 1 \end{cases}

$\\ \begin{cases} \alpha & = 0 \\ \beta & = 0 \\ \gamma & = 0 \\ \delta & = 1 \\ \end{cases}$

따라서 일반식을 적용하면 다음과 같이 된다.

\begin{aligned} R_{n} & = D (n) \\ = \frac{n (n + 1) (2 n + 1)}{6} \\ ∴ ◻_{n} & = \frac{n (n + 1) (2 n + 1)}{6} \end{aligned}

$\begin{align} R_n & = D(n) \\ & = { n(n+1)(2n+1) \over 6 } \\ \\ \therefore \Box_n & = { n(n+1)(2n+1) \over 6 } \\ \end{align}$

닫힌 형식을 구했다!

방법 4: 합을 적분으로 대체한다

Replace sums by integrals.

이산수학이 아니라 미적분을 배운 사람들은 $\sum$ 보다 $\int$ 이 더 익숙할 것이다.
교재의 목표는 독자가 $\sum$ 에 익숙해지는 것이다.
- 두 방식의 아이디어는 아주 비슷하다.

이를 밑변의 길이가 1이고 높이가 k^2인 직사각형들의 넓이의 합으로 생각할 수 있다.

\begin{aligned} ◻_{n} & = 0^{2} + 1^{2} + 2^{2} + . . . + n^{2} \\ = 1 \cdot 0^{2} + 1 \cdot 1^{2} + 1 \cdot 2^{2} + . . . + 1 \cdot n^{2} \\ = 밑 \cdot 높 + 밑 \cdot 높 + 밑 \cdot 높 + . . . + 밑 \cdot n^{2} \end{aligned}

$\begin{align} \Box_n & = 0^2 + 1^2 + 2^2 + ... + n^2 \\ & = 1 \cdot 0^2 + 1 \cdot 1^2 + 1 \cdot 2^2 + ... + 1 \cdot n^2 \\ & \color{gray}{= 밑 \cdot 높 + 밑 \cdot 높 + 밑 \cdot 높 + ... + 밑 \cdot n^2 } \\ \end{align}$

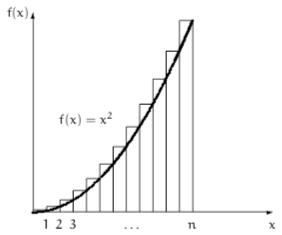
integral

$f(x) = x^2$
위의 그래프에서 곡선 아래쪽 면적의 넓이는 다음과 같다.
- $\int_0^n x^2 dx = \frac{1}{3} \cdot n^3$
그런데 $\Box_n$ 은 직사각형들의 넓이의 총합이므로, 곡선 아래쪽의 면적을 확인해야 할 필요가 있다.

즉, 다음과 같이 생각할 수 있다.

◻_{n} = 곡선 아래쪽의 넓이 + 곡선 위쪽 남은 부분들의 넓이

$\Box_n = \text{곡선 아래쪽의 넓이} + \text{곡선 위쪽 남은 부분들의 넓이}$

그리고 곡선 아래쪽의 넓이는 적분을 통해 구할 수 있다.

\begin{aligned} 곡선 아래쪽의 넓이 & = \int_{0}^{n} x^{2} d x \\ = \frac{1}{3} \cdot n^{3} \end{aligned}

$\begin{align} \text{곡선 아래쪽의 넓이} & = \int_0^n x^2 dx \\ & = \frac{1}{3} \cdot n^3 \\ \end{align}$

그렇다면 곡선 위쪽의 넓이만 구하면 된다.

곡선 위쪽의 넓이를 구하자

곡선 위쪽의 넓이 $E_n$ 은 다음과 같이 표현할 수 있다.

\begin{aligned} E_{n} & = ◻_{n} - 곡선 아래쪽의 넓이 \\ = ◻_{n} - \frac{1}{3} \cdot n^{3} \\ = (◻_{n - 1} + n^{2}) - \frac{1}{3} \cdot n^{3} \\ 한 편, & E_{n - 1} 를 정리해보면 다음을 알 수 있다. \\ E_{n - 1} = ◻_{n - 1} - \frac{1}{3} \cdot (n - 1)^{3} \\ ◻_{n - 1} = E_{n - 1} + \frac{1}{3} \cdot (n - 1)^{3} \\ E_{n - 1} 를 대입하자. \\ E_{n} & = (◻_{n - 1} + n^{2}) - \frac{1}{3} \cdot n^{3} \\ = (E_{n - 1} + \frac{1}{3} \cdot (n - 1)^{3} + n^{2}) - \frac{1}{3} \cdot n^{3} \\ = E_{n - 1} + \frac{1}{3} \cdot (n - 1)^{3} + n^{2} - \frac{1}{3} \cdot n^{3} \\ = E_{n - 1} + \frac{1}{3} \cdot (n^{3} - 3 n^{2} + 3 n - 1) + n^{2} - \frac{1}{3} \cdot n^{3} \\ = E_{n - 1} + \frac{- 3 n^{2} + 3 n - 1}{3} + \frac{3 n^{2}}{3} \\ = E_{n - 1} + \frac{3 n - 1}{3} \\ = E_{n - 1} + n - \frac{1}{3} \\ ∴ E_{n} & = E_{n - 1} + n - \frac{1}{3} \end{aligned}

$\require{cancel} \begin{align} E_n & = \Box_n - \text{곡선 아래쪽의 넓이} \\ & = \Box_n - \frac{1}{3} \cdot n^3 \\ & = (\Box_{n-1} +n^2) - \frac{1}{3} \cdot n^3 \\ \\ 한편, & \; E_{n-1} \text{를 정리해보면 다음을 알 수 있다.}\\ & E_{n-1} = \Box_{n-1} - \frac{1}{3} \cdot (n-1)^3 \\ & \color{red}{\Box_{n-1}} = E_{n-1} + \frac{1}{3} \cdot (n-1)^3 \\ & E_{n-1}\text{를 대입하자.} \\ \\ E_n & = (\color{red}{\Box_{n-1}} +n^2) - \frac{1}{3} \cdot n^3 \\ & = \left(\color{red}{E_{n-1} + \frac{1}{3} \cdot (n-1)^3} + n^2 \right) - \frac{1}{3} \cdot n^3 \\ & = E_{n-1} + \frac{1}{3} \cdot (n-1)^3 + n^2 - \frac{1}{3} \cdot n^3 \\ & = E_{n-1} + \frac{1}{3} \cdot (\cancel{n^3} - 3n^2 + 3n -1) + n^2 - \cancel{\frac{1}{3} \cdot n^3} \\ & = E_{n-1} + \frac{ \cancel{- 3n^2} + 3n -1}{3} + \cancel{\frac{3n^2}{3}} \\ & = E_{n-1} + \frac{3n -1}{3} \\ & = E_{n-1} + n - \frac{1}{3} \\ \\ \therefore E_n & = E_{n-1} + n - \frac{1}{3} \\ \\ \end{align}$

$E_0 = 0$ 이므로, $E_n$ 의 닫힌 형식은 다음과 같이 구할 수 있을 것이다.

\begin{aligned} E_{0} & = 0 \\ E_{1} & = 0 + 1 - \frac{1}{3} \\ E_{2} & = (0 + 1 - \frac{1}{3}) + 2 - \frac{1}{3} \\ . . . \\ 항이 하나 올라갈 때마다 n을 더하고 \frac{1}{3} 을 빼고 있다. \\ ∴ E_{n} & = \sum_{0 \leq k \leq n} k - \frac{1}{3} \cdot n \\ = \frac{n (n + 1)}{2} - \frac{1}{3} \cdot n \\ = \frac{n^{2} + n}{2} - \frac{n}{3} \\ = \frac{3 n^{2} + 3 n}{6} - \frac{2 n}{6} \\ = \frac{3 n^{2} + n}{6} \end{aligned}

$\begin{align} E_0 & = 0 \\ E_1 & = 0 + 1 - \frac{1}{3} \\ E_2 & = (0 + 1 - \frac{1}{3}) + 2 - \frac{1}{3} \\ ... \\ & \text{항이 하나 올라갈 때마다 n을 더하고 } \frac{1}{3} \text{을 빼고 있다.} \\ \\ \therefore E_n & = \sum_{0 \le k \le n} k - \frac{1}{3} \cdot n \\ & = \frac{n(n+1)}{2} - \frac{1}{3} \cdot n \\ & = \frac{n^2 + n}{2} - \frac{n}{3} \\ & = \frac{3n^2 + 3n}{6} - \frac{2n}{6} \\ & = \frac{3n^2 + n}{6} \\ \end{align}$

결과를 정리해 보자.

\begin{array}{cccc} ◻_{n} & = & 곡선 아래쪽의 넓이 & + & 곡선 위쪽 남은 부분들의 넓이 \\ = & \frac{n^{3}}{3} & + & \frac{3 n^{2} + n}{6} \end{array}

$\begin{array}{cccc} \Box_n & = & \text{곡선 아래쪽의 넓이} & + & \text{곡선 위쪽 남은 부분들의 넓이} \\ & = & \frac{n^3}{3} & + & \frac{3n^2 + n}{6} \\ \end{array}$

이제 답을 구할 수 있을 것 같다.

\begin{aligned} ◻_{n} & = \frac{n^{3}}{3} + \frac{3 n^{2} + n}{6} \\ = \frac{2 n^{3}}{6} + \frac{3 n^{2} + n}{6} \\ = \frac{2 n^{3} + 3 n^{2} + n}{6} \\ = \frac{n (2 n^{2} + 3 n + 1)}{6} \\ = \frac{n (n + 1) (2 n + 1)}{6} \end{aligned}

$\begin{align} \Box_n & = \frac{n^3}{3} + \frac{3n^2 + n}{6} \\ & = \frac{2n^3}{6} + \frac{3n^2 + n}{6} \\ & = \frac{2n^3 + 3n^2 + n}{6} \\ & = {n(2n^2 + 3n + 1) \over 6} \\ & = {n(n+1)(2n+1) \over 6} \\ \end{align}$

닫힌 형식을 구했다!

곡선 위쪽의 넓이를 적분으로 구하자

문제는 풀었지만, 곡선 위쪽의 넓이를 적분으로 구하는 것도 연습할 가치가 있을 것 같다.

이것도 해보자.

곡선 위쪽의 넓이 $E_n$ 을 다음과 같이 표현하는 것도 가능할 것이다.

\begin{aligned} E_{n} & = 0번째 직사각형의 넓이 - 0번째 직사각형 곡선 아래쪽 넓이 \\ + 1번째 직사각형의 넓이 - 1번째 직사각형 곡선 아래쪽 넓이 \\ + 2번째 직사각형의 넓이 - 2번째 직사각형 곡선 아래쪽 넓이 \\ . . . \\ + n번째 직사각형의 넓이 - n번째 직사각형 곡선 아래쪽 넓이 \\ = \sum_{1 \leq k \leq n} (k^{2} - \int_{k - 1}^{k} x^{2} d x) \\ = \sum_{1 \leq k \leq n} (k^{2} - (\frac{k^{3}}{3} - \frac{(k - 1)^{3}}{3})) \\ = \sum_{1 \leq k \leq n} (\frac{3 k^{2}}{3} - \frac{k^{3}}{3} + \frac{(k - 1)^{3}}{3}) \\ = \frac{1}{3} \sum_{1 \leq k \leq n} (3 k^{2} - k^{3} + (k - 1)^{3}) \\ = \frac{1}{3} \sum_{1 \leq k \leq n} (3 k^{2} - k^{3} + k^{3} - 3 k^{2} + 3 k - 1) \\ = \frac{1}{3} \sum_{1 \leq k \leq n} (3 k - 1) \\ = \frac{1}{3} (\sum_{1 \leq k \leq n} 3 k - \sum_{1 \leq k \leq n} 1) \\ = \frac{1}{3} (3 \sum_{1 \leq k \leq n} k - n) \\ = \frac{1}{3} (3 \cdot \frac{n (n + 1)}{2} - n) \\ = \frac{n (n + 1)}{2} - \frac{n}{3} \\ = \frac{3 n (n + 1)}{6} - \frac{2 n}{6} \\ = \frac{3 n^{2} + 3 n}{6} - \frac{2 n}{6} \\ = \frac{3 n^{2} + n}{6} \\ ∴ E_{n} & = \frac{3 n^{2} + n}{6} \end{aligned}

$\require{cancel} \begin{align} E_n & = \text{0번째 직사각형의 넓이 - 0번째 직사각형 곡선 아래쪽 넓이} \\ & \quad + \text{1번째 직사각형의 넓이 - 1번째 직사각형 곡선 아래쪽 넓이} \\ & \quad + \text{2번째 직사각형의 넓이 - 2번째 직사각형 곡선 아래쪽 넓이} \\ & \quad ... \\ & \quad + \text{n번째 직사각형의 넓이 - n번째 직사각형 곡선 아래쪽 넓이} \\ \\ & = \sum_{1 \le k \le n} \left( k^2 - \int_{k-1}^{k} x^2 dx \right)\\ & = \sum_{1 \le k \le n} \left( k^2 - \left( \color{red}{\frac{k^3}{3} - \frac{(k-1)^3}{3}} \right) \right)\\ & = \sum_{1 \le k \le n} \left( \frac{3k^2}{3} - \frac{k^3}{3} + \frac{(k-1)^3}{3} \right)\\ & = \frac{1}{3} \sum_{1 \le k \le n} \left( 3k^2 - k^3 + (k-1)^3 \right)\\ & = \frac{1}{3} \sum_{1 \le k \le n} \left( \cancel{3k^2} - \cancel{k^3} + \cancel{k^3} - \cancel{3k^2} + 3k - 1 \right)\\ & = \frac{1}{3} \sum_{1 \le k \le n} \left( 3k - 1 \right)\\ & = \frac{1}{3} \left( \sum_{1 \le k \le n} 3k - \sum_{1 \le k \le n} 1 \right) \\ & = \frac{1}{3} \left( 3 \sum_{1 \le k \le n} k - n \right) \\ & = \frac{1}{3} \left( 3 \cdot \frac{n(n+1)}{2} - n \right) \\ & = \frac{n(n+1)}{2} - \frac{n}{3} \\ & = \frac{3n(n+1)}{6} - \frac{2n}{6} \\ & = \frac{3n^2+3n}{6} - \frac{2n}{6} \\ & = \frac{3n^2+n}{6} \\ \\ \therefore E_n & = \frac{3n^2+n}{6} \\ \end{align}$

윗 절에서 구한 $E_n$ 과 똑같다.

책에 있는 학생 주석엔 "미적분에 중독된 사람들을 위한 방법이다.(This is for people addicted to calculus.)" 라고 되어 있었지만, 이 방법이 더 쉽고 간편한 것 같다.

그 외의 방법들 (방법 6, 7)

다음 방법들은 이번 챕터에서 배우지 않고 다음 챕터에서 배운다.

방법 6: 유한 미적분을 사용한다. (Method 6: Use finite calculus.)
- 2.6 유한-무한 미적분에서 배운다.
방법 7: 생성함수를 사용한다. (Method 7: Use generating functions.)
- 5.4 생성함수에서 배운다.

개요

방법 0: 답을 찾아본다

방법 1: 답을 추측하고 귀납법으로 증명한다

방법 2: 합을 어지럽힌다(섭동)

방법 3: 레퍼토리를 구축한다

일반식 만들기

문제를 해결하기

방법 4: 합을 적분으로 대체한다

곡선 위쪽의 넓이를 구하자

곡선 위쪽의 넓이를 적분으로 구하자

그 외의 방법들 (방법 6, 7)

Links