암달의 법칙 (Amdahl's law)
S = 1 / ((1-f) + f/s)
역사
Gene Amdahl, 1922 ~ 2015
- 미국의 컴퓨터 공학자.
- IBM에서 메인프레임 개발에 크게 공헌했다.
암달의 법칙
- "Validity of the single processor approach to achieving large scale computing capabilitie"
- 유명한 수식은 논문에는 포함되어 있지 않다.
- 약 2~3장 분량의 짧은 논문이고, 읽어보면 단순한 그래프 하나가 첨부되어 있다.
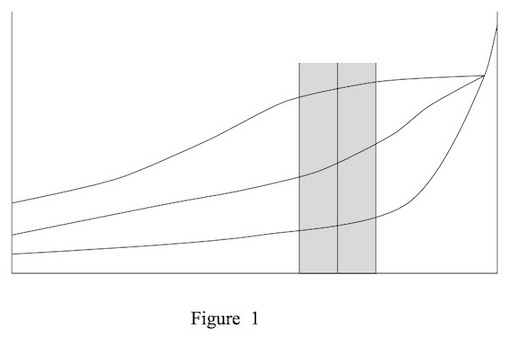
다음은 암달의 논문에 수록된 그래프를 SSCS News의 에디터들이 다시 그린 것이다.
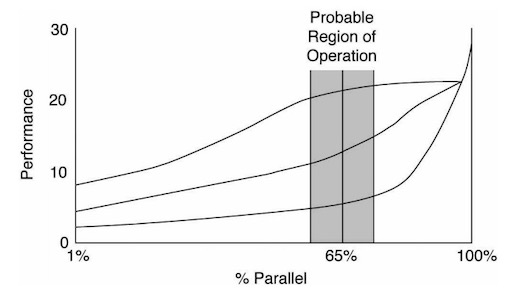
정의
Amdahl' s Law summarizes the performance improvement of some process, such as a computer program. It considers that in order to improve performance (time to complete the process), only a part of the entire process is usually improved. It shows that the improvement is limited by the fraction of time the improved part is used. It can be stated in terms of two parameters: , the fraction of time spent in the improved part, and the speedup , how many times faster the improved part performs. Amdahl's Law gives how many times faster the entire process will be as \(S_\text{overall} = { 1 \over (1-f) + \frac{f}{s} }\).
위의 글은 Wolfram Demonstrations Project Amdahl's Law의 글을 인용한 것이다.1
내용을 정리해 보자면 다음과 같다.
암달의 법칙은 컴퓨터 프로그램 같은 프로세스의 성능 향상에 대한 정보를 제공한다.
- 암달의 법칙에서 다루는 성능(performance)은 시간이 기준이다.
- 프로세스 완료까지의 소요 시간.
- 일반적으로 성능을 향상시키기 위해, 전체가 아닌 일부 프로세스의 개선 작업이 이루어지곤 한다.
- 개선된 부분은 시스템의 일부이므로, 사용되는 시간의 비율 때문에 개선에 한계점이 있다.
암달의 법칙은 두 개의 매개변수로 이러한 현상을 설명한다.
- \(f\): 전체 시스템 시간에서 개선된 부분이 차지하고 있는 시간의 비율.
- \(S\): 성능이 몇 배 향상됐는지.
암달의 법칙은 이를 통해 전체 프로세스가 몇 배 빨라졌는지를 다음 식으로 보여준다.
\[S_\text{latency} = { 1 \over (1-f) + \frac{f}{s} }\]예제: 함수 하나의 성능을 2배로 개선한 결과
다음과 같은 프로파일 정보가 있다고 하자.
| 항목 | 수행 시간 |
|---|---|
execute 함수 |
6분 |
execute외의 모든 부분 |
4분 |
| 전체 프로그램 | 10분 |
그래서 A 개발자가 execute 함수를 2배 빠르게 개선해서, 3분 만에 끝나게 만들었다고 하자.
이 정보를 통해 두 파라미터의 값이 다음과 같다는 사실을 알 수 있다.
- 전체 시스템에서
execute의 비율. \(f = {6 \over 10} = 0.6\). execute가 몇 배 빨라졌는지. \(s = 2\).
이제 식에 대입하면 된다.
\[S = { 1 \over ( 1 - 0.6 ) + \frac{0.6}{2} } = { 1 \over 0.7 } = 1.4285...\]execute를 2배 빠르게 만든 결과 시스템 전체의 성능이 \(10 \over 7\)배, 즉 약 1.4285...배 향상됐다는 것을 알 수 있다.
개선 작업 이후의 타임 테이블을 다음과 같이 작성해 보면 간단하게 식을 검증해 볼 수 있다.
| 항목 | 수행 시간(before) | 수행 시간(after) |
|---|---|---|
execute외의 모든 부분 |
4분 | 4분 (변하지 않았음) |
execute 함수 |
6분 | 3분 (2배 빨라짐) |
| 전체 프로그램 | 10분 | 7분 |
전체 프로그램의 수행 시간이 10분에서 7분이 되었으므로 \(10 \over 7\)배로 성능이 향상됐다.
예제: 성능 향상의 한계
한편, A 개발자의 옆 팀에서 일하고 있던 B 개발자는 execute 함수가 필요없다는 사실을 발견했다.
그래서 execute 함수의 내용을 삭제해서 아무 일도 하지 않게 만들었고, 전체 수행시간이 4분으로 감소됐다고 하자.
그렇다면 시스템 전체의 성능은 \(10 \over 4\) 배, 즉 2.5배 향상되었을 것이다.
| 항목 | 수행 시간(before) | 수행 시간(after) |
|---|---|---|
execute외의 모든 부분 |
4분 | 4분 (변하지 않았음) |
execute 함수 |
6분 | 0분 (더이상 빨라질 수 없음) |
| 전체 프로그램 | 10분 | 4분 |
식으로도 나타내 보자.
- 전체 시스템에서
execute의 비율. \(f = {6 \over 10} = 0.6\). execute가 몇 배 빨라졌는지. \(s = \lim_{n \to \infty} n\).
이 결과를 통해 execute 함수를 개선해서 얻을 수 있는 시스템 전체의 성능 향상 한계가 2.5배라는 사실을 알 수 있다.
병렬 처리 버전
위의 식은 두 파라미터의 정의를 교체하면 병렬 버전으로도 의미를 갖는다.
\[S_\text{latency} = { 1 \over (1-f) + \frac{f}{n} }\]- \(f\): 전체 시스템 시간에서 병렬화 가능한 부분이 차지하고 있는 시간의 비율.
- \(n\): 병렬화 (프로세서) 개수.
이를 통해 이론적인 성능 향상의 최대값은 병렬화 가능한 부분이 얼마나 차지하는지에 영향을 받는다는 것을 알 수 있다.
인용
From: 위키백과
다음은 영문 위키백과 Amdahl's law에 첨부된 이미지이다.
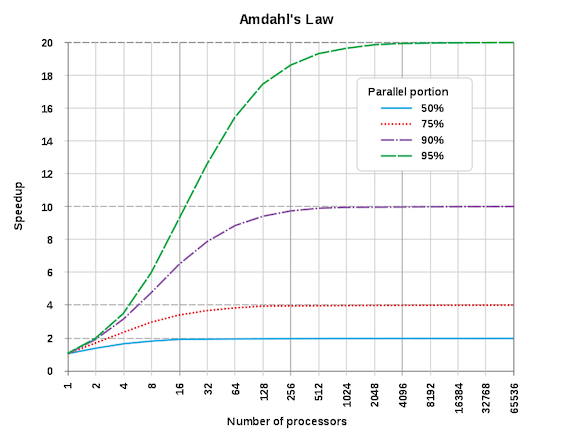
The theoretical speedup of the latency of the execution of a program as a function of the number of processors executing it, according to Amdahl's law. The speedup is limited by the serial part of the program. For example, if 95% of the program can be parallelized, the theoretical maximum speedup using parallel computing would be 20 times.
한국어 위키백과 암달의 법칙에는 다음과 같이 번역되어 있다.
병렬 컴퓨팅에서 멀티 프로세서를 사용할 때 프로그램의 성능향상은 프로그램의 순차적인 부분에 의해 제한된다. 예를 들면, 프로그램의 95%가 병렬화 할 수 있다면 이론적인 최대 성능 향상은 아무리 많은 프로세서를 사용하더라도 최대 20배로 제한된다.
From: 프로그래머가 몰랐던 멀티코어 CPU 이야기
- 암달의 법칙의 심오한 의미
이 문제는 컴퓨터 공학에서 많은 것을 생각하게 해준다. 아무리 최적화를 하더라도 이 최적화로부터 영향받지 않는 다른 부분으로 그 효과는 제한적일 수 있다는 것이다. 이것이 바로 암달의 법칙(Amdahl's law)이다.
(중략)
암달의 법칙은 간단하지만, 꽤 심오한 의미가 있다. 프로그래머가 프로그램 성능을 개선할 때 헛된 곳에 시간을 낭비하지 말고 가장 많은 시간이 소요되는 곳에 집중해야 함을 말한다. 프로세서 설계자 역시 자신이 최적화하려는 부분이 전체에서 얼마나 중요한지 잘 생각하고 우선순위를 결정해야 한다. 결국 2장에서 이야기한 컴퓨터 구조 설계의 가장 중요한 법칙인, '흔한 경우를 빠르게 하라(Make the common case fast)'와 일맥상통한다. 2
- 병렬 프로그래밍 버전
따라서 암달의 법칙, 수식 4-1을 병렬 프로그래밍 버전으로 고치면 다음과 같다.
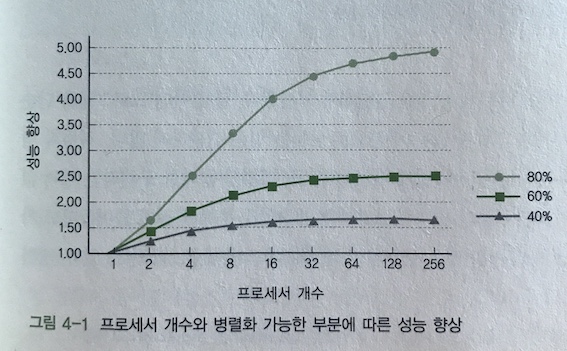
\[1 \over (1-P) + \frac{P}{N}\]수식 4-2에서 P는 전체 프로그램 중 병렬화 가능한 부분, N은 프로세서 개수를 가리킨다. 물론 이 공식은 프로세서 N이 완벽하게 P만큼의 일을 병렬 처리한다는 매우 이상적인 가정을 하고 있다. 암달의 법칙으로 병렬화 가능한 부분이 80%, 60%, 40%일 때 얻을 수 있는 이상적인 성능 향상 곡선을 생각해보자. 그림 4-1에 이 결과가 나타나 있다.
그림 4-1에서 보듯이 만약 자신의 프로그램 중 40%만 병렬화가 가능하다면 아무리 많은 프로세서가 있다 하더라도 성능 향상은 채 두 배도 될 수 없다. 또 80% 이상 병렬화 할 수 있다해도 성능을 다섯 배 이상 향상시킬 수는 없다.병렬화 문제에서도 암달의 법칙은 매우 중요한 과제를 준다. 병렬화 가능한 부분을 효율적으로 병렬화하여 최적의 성능을 얻는 것도 중요하지만, 무엇보다 병렬화 가능한 부분을 극대화, 다시 말해 직렬로 처리해야 하는 부분(\(1-P\))을 줄이는 것이 핵심이다. 과학이나 수학 관련 프로그램은 수행 시간의 대부분을 순환문이 차지하며 병렬 가능한 경우가 많다. 어떤 경우는 완벽히 - 어떤 뮤텍스나 동기화도 필요 없이 - 병렬화가 가능하기도 하고 어떤 때는 동기화가 필요하기도 하지만, 어찌 되었든 수행 시간의 대부분이 병렬화로 도움을 얻을 수 있다. 이런 응용프로그램은 \(1-P\)가 꽤 작다. 그러나 그렇지 않은 프로그램 역시 많다. 컴파일러나 운영체제의 주요 코드는 연산이 직렬로 수행되는 경우가 많다. 3
From: Beautiful Code
행렬 자료를 분할하다 보니 소위 암달의 법칙(Amdahl's law)이 말하는 규모가변성 문제가 금세 드러나게 되었다. 암달의 법칙이란 한 계산에서 순차적인 부분에 소요되는 시간이 전체 수행 시간의 최소 하계를(따라서 병렬 처리로 얻을 수 있는 이득을) 결정한다는 것이다. 바꾸어 말하자면, 대부분의 게산들이 독립적으로 수행되지 않는 한, 하드웨어 구성에 프로세서들을 추가한다고 해도 처리가 더 빨라지지는 않는 이득체감 지점에 도달한다는 것이다. 4
From: 자바 병렬 프로그래밍
대부분의 병렬 프로그램에는 병렬화할 수 있는 작업과 순차적으로 처리해야 하는 작업이 뒤섞인 단위 작업의 덩어리를 갖고 있다. 암달의 법칙(Amdahl's law)을 사용하면 병렬 작업과 순차 작업의 비율에 따라 하드웨어 자원을 추가로 투입했을 때 이론적으로 속도가 얼마나 빨라질지에 대한 예측 값을 얻을 수 있다. 암달의 법칙에 따르면, 순차적으로 실행돼야 하는 작업의 비율을 \(F\)라 하고 하드웨어에 꽂혀 있는 프로세서의 개수를 \(N\)이라고 할 때, 다음의 수식에 해당하는 정도까지 속도를 증가시킬 수 있다.
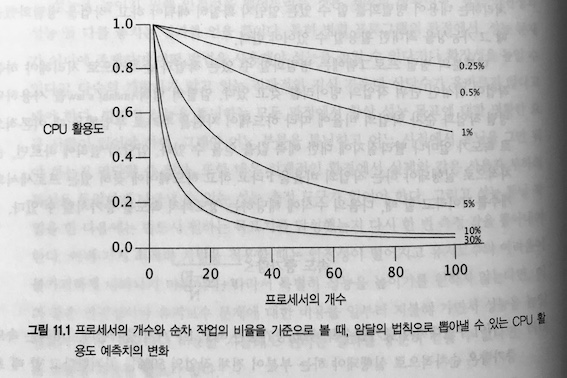
\[\text{ Speedup } \le { 1 \over F + \frac{ (1-F) }{N} }\]\(N\)이 무한대까지 증가할수록 속도 증가량은 최고 \(1/F\) 까지 증가한다. \(1/F\)라는 속도 증가량은 순차적으로 실행돼야 하는 부분이 전체 작업의 50%를 차지한다고 할 때 프로세서를 아무리 많이 꽂는다 해도 겨우 두 배 빨라진다는 결과이다. 그리고 순차적으로 실행해야 하는 부분이 전체의 10%에 해당한다면 최고 10배까지 속도를 증가시킬 수 있다고 예측할 수 있다. 암달의 법칙을 활용하면 작업을 순차적으로 처리하는 부분이 많아질 때 느려지는 정도가 얼마만큼인지를 수치화할 수 있다. 하드웨어에 CPU가 10개 꽂혀 있을 때, 10%의 순차 작업을 갖고 있는 프로그램은 최고 5.3배 만큼의 속도를 증가(CPU 활용도는 5.3배/10개 = 0.53, 즉 53%)시킬 수 있다. 같은 상황에서 CPU를 100개를 꽂는다면 최대 9.2배까지 속도가 증가(CPU 활용도는 9.2배/100개 = 0.092, 즉 9.2%)할 것이라고 예상할 수 있다. 그러다 보니, 속도를 최대 10배까지 증가시키려면 CPU의 활용도가 너무나 비효율적으로 떨어질 수밖에 없다.
그림 11.1을 보면 순차적인 작업의 비율과 프로세서의 개수를 놓고 볼 때 프로세서 활용도가 어떻게 변하는지를 한눈에 볼 수 있다(CPU 활용도는 속도 증가량을 프로세서의 개수로 나눈 값이라고 정의한다). 암달의 법칙에 따르면 프로세서의 개수가 증가하면 할 수록, 순차적으로 실행해야 하는 부분이 아주 조금이라도 늘어나면 프로세서 개수에 비해 얻을 수 있는 속도 증가량이 크게 떨어진다.
애플리케이션의 작업을 작은 단위 작업으로 분할하는 방법에 대해서는 이미 6장에서 살펴본 바가 있다. 하지만 멀티프로세서 시스템에서 애플리케이션을 실행할 때 속도가 얼마만큼 빨라질 것인지에 대한 예측을 해보려면, 애플리케이션 내부에서 순차적으로 처리해야 하는 작업이 얼마나 되는지를 먼저 확인해야 한다. 5
참고문헌
도서
- Beautiful Code / 찰스 페졸드 외 37 저 / 한빛미디어 / 초판발행 2007년 12월 17일 (2020년 기준 절판)
- 자바 병렬 프로그래밍 / 브라이언 게츠 등저 / 에이콘출판사 / 2쇄 발행 2016년 03월 22일 / 원제: Java Concurrency in Practice
- 프로그래머가 몰랐던 멀티코어 CPU 이야기 / 김민장 저 / 한빛미디어 / 2010년 05월 28일 (2020년 기준 절판)
웹 문서
- Validity of the single processor approach to achieving large scale computing capabilitie - Gene M. Amdahl (PDF)
- Validity of the single processor approach to achieving large scale computing capabilitie - Gene M. Amdahl (PDF) - Guihai Chen이 옮겨 적은 버전. (This paper is retyped as the present form by Guihai Chen He wishes you would enjoy reading this historic)