• MATHEMATICAL PRELIMINARIES AND NOTATION
  • 수학적 개요 및 표기법

집합(Sets)

원소(elements)들의 모임.

대체로 중학교에서 배우는 내용이다.

  • x가 집합 S의 원소
\[x \in S\]
  • 정수 0, 1, 2 를 포함하는 집합
\[S = \{ 0, 1, 2 \}\]
  • 의미가 명확하면 생략 기호 \(...\)를 쓸 수 있다.
\[\begin{align} \text{모든 소문자의 집합} & = \{ a, b, ..., z \} \\ \text{양의 정수 짝수들의 집합} & = \{ 2, 4, 6, ... \} \\ \end{align}\]
  • 다음과 같이 표현할 수도 있다.
    • "S는 0보다 크고 짝수인 모든 i의 집합, i는 정수."
\[S = \{ i : i \gt 0, \text{ i is even } \}\]
  • 합집합(union, \(\cup\))
\[S_1 \cup S_2 = \{ x : x \in S_1 \ or \ x \in S_2 \}\]
  • 교집합(intersection, \(\cap\))
\[S_1 \cap S_2 = \{ x : x \in S_1 \ and \ x \in S_2 \}\]
  • 차집합(difference, \(-\))
\[S_1 - S_2 = \{ x : x \in S_1 \ and \ x \notin S_2 \}\]
  • 여집합(complementation)
    • 전체 집합 U 가 정의된 상태에서,
\[\overline{S} = \{ x : x \in U, x \notin S \}\]
  • 공집합(empty set, null set)
\[\varnothing\]
  • 집합의 정의로부터 알 수 있는 것들
\[\begin{align} S \cup \varnothing & = S - \varnothing = S \\ S \cap \varnothing & = \varnothing \\ \overline{ \varnothing } & = U \\ \overline{\overline{S}} & = S \\ \end{align}\]

DeMorgan의 법칙

\[\begin{align} \overline{S_1 \cup S_2} & = \overline{S_1} \cap \overline{S_2} \\ \overline{S_1 \cap S_2} & = \overline{S_1} \cup \overline{S_2} \\ \end{align}\]

부분집합

  • 부분집합(subset)
\[S_1 \subseteq S\]
  • 진부분집합(proper subset)
    • \(S_1 \subseteq S\)이면서 \(S\)가 \(S_1\)에 없는 원소를 포함하는 경우.
\[S_1 \subset S\]
  • 서로소(disjoint)
    • 두 집합 사이에 공통으로 속하는 원소가 없는 경우.
    • 즉, \(S_1 \cap S_2 = \varnothing\)인 경우.
  • 무한 집합(infinite set) : 원소의 개수가 무한한 경우.
  • 유한 집합(finite set) : 원소의 개수가 유한한 경우.
  • 유한 집합의 크기
    • 집합의 원소의 개수
\[| S |\]

멱집합

  • 멱집합(powerset)
    • 한 집합 S의 모든 부분 집합들의 집합.
    • 집합을 원소로 삼는 집합이라는 점에 주목.
\[2^S\]

예를 들어 집합 \(S = \{ a, b, c \}\)의 멱집합은 다음과 같다.

\[2^S = \{ \varnothing, \{ a \}, \{ b \}, \{ c \}, \{ a, b \}, \{ a, c \}, \{ b, c \}, \{ a, b, c \} \}\]

곱집합

  • 곱집합(Cartesian product, 데카르트 곱, 카티지언 프로덕트)
    • 다른 여러 집합 원소들의 순서열(ordered sequence)을 원소로 갖는 집합.
    • 두 집합의 카티션 곱은 순서쌍(ordered pair)들의 집합이 된다.
\[\begin{align} S & = S_1 \times S_2 \\ & = \{ (x,y) : x \in S_1, y \in S_2 \} \\ \end{align}\]

예를 들어 두 집합 \(S_1, S_2\)이 다음과 같을 때,

\[\begin{align} S_1 & = \{ 10, 20 \} \\ S_2 & = \{ 1, 2, 3, 4 \} \\ \end{align}\]

카티션 곱은 다음과 같다.

\[\begin{align} S_1 \times S_2 & = \{ (10, 1), (10, 2), (10, 3), (10, 4), (20, 1), (20, 2), (20, 3), (20, 4) \} \\ \end{align}\]
  • 주의: 순서쌍 내 원소의 순서가 바뀌면 안 된다.
  • (10, 2)는 있지만 (2, 10)은 안 됨. 완전히 의미가 바뀐다.

둘 이상의 집합에 대한 카티션 곱.

\[S_1 \times S_2 \times ... \times S_n = \{ (x_1, x_2, ..., x_n) : x_i \in S_i \}\]

분할

집합은 여러 부분집합으로 분할할 수 있다.

\(S_1, S_2, ..., S_n\)이 \(S\)의 부분집합이고 다음의 조건들을 만족한다면…

  • 부분집합 \(S_1, S_2, ..., S_n\) 은 모두 공유하는 원소가 없다.
    • 모두 서로소(mutually disjoint)이다.
  • \(S_1 \cup S_2 \cup ... \cup S_n = S\).
  • \(S_i\)중 어느 집합도 공집합이 아니다.

\(S_1, S_2, ..., S_n\)를 \(S\)의 분할(partition)이라 한다.

함수와 관계(Functions and Relations)

  • 함수(function) : 집합의 원소들 각각에 대해 다른 집합의 단일 원소로 배정하는 규칙.
  • \(f\)가 함수라면, 첫 번째 집합을 함수 \(f\)의 정의역(domain)이라 하고, 두 번째 집합을 치역(range)이라 한다.
  • 함수 \(f\)는 다음과 같이 표기한다.
\[f : S_1 \rightarrow S_2\]
  • 위와 같이 표기한다면 다음을 의미한다.
    • 함수 \(f\)의 정의역은 \(S_1\)의 부분집합이다.
    • 함수 \(f\)의 치역은 \(S_2\)의 부분집합이다.

전체 함수, 부분 함수

  • 전체 함수(total function): 함수 \(f\)의 정의역이 \(S_1\)과 같다면 \(f\)를 전체 함수라 한다.
  • 부분 함수(partial function): \(f\)가 전체 함수가 아닌 경우.

크기 순위 표기법(order-of-magnitude notation)

  • \(f(n)\)과 \(g(n)\)이 정의역이 양의 정수들의 부분집합인 함수라 하자.

\(O\)

충분히 큰 모든 n에 대하여, 다음의 부등식을 만족하는 양의 상수 c가 존재한다면,

\[f(n) \le c | g(n) |\]

\(f\)의 순위가 \(g\)의 순위보다 높지 않다고 한다(we say that \(f\) has order at most \(g\)).

그리고 다음과 같이 표기한다.

\[f(n) = O(g(n))\]

\(\Omega\)

충분히 큰 모든 n에 대하여, 다음의 부등식을 만족하는 양의 상수 c가 존재한다면,

\[|f(n)| \ge c | g(n) |\]

\(f\)의 순위가 \(g\)의 순위보다 낮지 않다고 한다(then \(f\) has order at least \(g\)).

그리고 다음과 같이 표기한다.

\[f(n) = \Omega(g(n))\]

\(\Theta\)

충분히 큰 모든 n에 대하여, 다음의 부등식을 만족하는 상수 \(c_1, c_2\)가 존재한다면,

\[c_1 | g(n) | \le | f(n) | \le c_2 | g(n) |\]

\(f\)가 \(g\)와 같은 크기 순위를 갖는다고 한다(\(f\) and \(g\) have the same order of magnitude).

그리고 다음과 같이 표기한다.

\[f(n) = \Theta(g(n))\]
예제

다음과 같은 함수가 있다.

\[\begin{align} f(n) & = 2n^2 + 3n, \\ g(n) & = n^3, \\ h(n) & = 10n^2 + 100. \\ \end{align}\]

크기 순위 표기법은 다음과 같다.

\[\begin{align} f(n) & = O(g(n)) \\ g(n) & = \Omega(h(n)) \\ f(n) & = \Theta(h(n)) \\ \end{align}\]

즉, 다음과 같이 생각할 수 있다.

\[\begin{align} 2n^2 + 3n & = O(n^3) \\ n^3 & = \Omega(10n^2 + 100) \\ 2n^2 + 3n & = \Theta(10n^2 + 100) \\ \end{align}\]
TAOCP도 찾아보자

좀 더 이해를 돕기 위해 TAOCP 1권의 1.2.11.1 O 표기법 챕터를 찾아보자.

Let’s look at some more examples. We know that

그럼 예들을 좀 더 보자. 다음은 우리가 알고 있는 것이다.

\[1^2 + 2^2 + ... + n^2 = \frac{1}{3}n(n + \frac{1}{2})(n+1) = \frac{1}{3}n^3 + \frac{1}{2}n^2 + \frac{1}{6}n\]

so it follows that

이로부터 다음을 얻는다.

\[\begin{align} 1^2 + 2^2 + ... + n^2 & = O(n^4) & \quad (2) \\ 1^2 + 2^2 + ... + n^2 & = O(n^3) & \quad (3) \\ 1^2 + 2^2 + ... + n^2 & = \frac{1}{3}n^3 + O(n^2) & \quad (4) \\ \end{align}\]

Equation (2) is rather crude, but not incorrect; Eq. (3) is a stronger statement; and Eq. (4) is stronger yet.

식 (2)가 상당히 대략적이긴 하지만, 그렇다고 부정확한 것은 아니다. 식 (3)은 좀 더 엄정한 서술이다. 그리고 식 (4)는 더욱 엄정하다.

(중략)

The O-notation is a big help in approximation work, since it describes briefly a concept that occurs often and it suppresses detailed information that is usually irrelevant. Furthermore, it can be manipulated algebraically in familiar ways, although certain important differences need to be kept in mind. The most important consideration is the idea of one-way equalities: We write \(\frac{1}{2}n^2 + n = O(n^2)\), but we never write \(O(n^2) = \frac{1}{2}n^2 + n\). (Or else, since \(\frac{1}{4}n^2 = O(n^2)\), we might come up with the absurd relation \(\frac{1}{4}n^2 = \frac{1}{2}n^2 + n\).) We always use the convention that the right-hand side of an equation does not give more information than the left-hand side; the right-hand side is a “crudification” of the left.

O 표기법은 자주 나타나는 개념을 간략히 서술하고 대체로 별 상관이 없는 세부 정보를 숨긴다는 점에서 근사를 다룰 때 큰 도움이 된다.

더 나아가서, 이 O들을 익숙한 대수적 방법으로 조작하는 것이 가능하다.

단, 몇 가지 중요한 차이들은 염두에 두어야 하는데, 가장 중요한 것이 단방향 상등(one-way equality)이라는 개념이다.

즉, \(\frac{1}{2}n^2 + n = O(n^2)\)이라고 쓸 수는 있지만 \(O(n^2) = \frac{1}{2}n^2 + n\)이라고는 절대 쓸 수 없다.

(만일 그런 표기가 허용된다면, \(\frac{1}{4}n^2 = O(n^2)\)이므로 \(\frac{1}{4}n^2 = \frac{1}{2}n^2 + n\)이라는 터무니없는 결과가 나온다.)

이 표기법이 관련된 등식에서는 항상 등식의 우변이 좌변보다 더 자세한 정보를 제공하지 않는다는 관례를 사용한다.

즉, 우변은 항상 좌변보다 조악한 버전인 것이다.

관계

함수를 순서쌍의 집합으로 표현할 수 있다.

\[\{ (x_1, y_1), (x_2, y_2), ... \}\]
  • 관계(relation)
    • 순서쌍의 집합으로 함수를 표현하려면 각 \(x_i\)가 이 집합 내에서 순서쌍의 첫 번째 위치에 한 번만 나타나야 한다.
    • 이 조건이 만족되지 않는 경우에는 이 집합을 관계라 부른다.
      • 즉, x 값 하나가 여러 개의 y 값을 갖는 경우를 순서쌍으로 나타낸 집합을 관계라 부른다.

동치 관계

\[x \equiv y\]

동치 관계(equivalence relation)는 세 가지 성질을 만족하는 경우를 말한다.

  • 반사성(reflexivity rule)
\[x \equiv x \ \text{ for all } x;\]
  • 대칭성(symmetry rule)
\[\text{if } x \equiv y, \text{ then } \ y \equiv x;\]
  • 전이성(transitivity rule)
\[\text{if } x \equiv y \ \text{ and } \ y \equiv z, \ \text{then} \ x \equiv z\]
예제

다음과 같은 음이 아닌 정수 집합에서의 관계를 정의하자.

\[x \equiv y \\ \text{if and only if} \\ x \text{ mod } 3 = y \text{ mod } 3 \\\]

이는 대략 다음과 같은 의미이다.

  • \(x \equiv y\) 이면 \(x \text{ mod } 3 = y \text{ mod } 3\) 라고 정의하자.

이 관계에서는 \(2 \equiv 5, 12 \equiv 0, 0 \equiv 36\) 등이 성립한다.

If S is a set on which we have a defined equivalence relation, then we can use this equivalence to partition the set into equivalence classes. Each equivalence class contains all and only equivalent elements.

  • 만약 집합 S에 동치관계가 정의되어 있다면, 이러한 동치성을 사용하여 집합 S를 동치부류(equivalence classes)로 분할할 수 있다.
  • 각각의 동치부류는 서로 동치인 원소들만을 포함한다.

그래프와 트리(Graphs and Trees)

  • 그래프 : 두개의 유한 집합으로 이루어지는 구조.
    • 정점(vertex)들의 집합. \(V = \{ v_1, v_2, ..., v_n \}\)
    • 간선(edge)들의 집합. \(E = \{ e_1, e_2, ..., e_m \}\)

예: 정점 \(v_j, v_k\)를 잇는 간선 \(e_i = (v_j, v_k)\)

  • \(v_j\) 기준으로 \(e_i\)는 진출 간선(outgoing edge).
  • \(v_k\) 기준으로 \(e_i\)는 진입 간선(incoming edge).

유향 그래프(digraph)

각 간선에 방향을 지정하는 그래프를 유향 그래프(directed graph, digraph)라 부른다.

라벨 그래프(labeled graph)

  • 정점이나 간선에 라벨(label)을 지정한 그래프.

그래프 도식화

  • 정점은 원으로 표현한다.
  • 간선은 두 정점을 잇는 화살표로 표현한다.

다음은 \(V = \{ v_1, v_2, v_3 \}\)이고, \(E = \{ (v_1, v_3), (v_3, v_1), (v_3, v_2), (v_3, v_3) \}\)인 그래프이다.

v₁ v₃ v₂

  • 보행(walk): \((v_i, v_j), (v_j, v_k), ..., (v_m, v_n)\) 와 같이 표현되는 간선들의 순서열을 \(v_i\)로부터 \(v_n\)으로의 보행(walk)라 한다.

  • 보행의 길이(length of a walk): 보행의 시작 정점부터 마지막 정점까지 지나게 되는 간선들의 수.

  • 경로(path): 어느 간선도 중복되지 않는 보행을 경로라 한다.

  • 단순 경로(simple path): 어느 정점도 중복하여 지나지 않는 경로.
    • 예: \((v_1, v_3), (v_3, v_2)\)
  • \(v_i\)를 base로 삼는 사이클(cycle): 정점 \(v_i\)로부터 어느 간선도 중복하여 지나지 않고 자신에게 돌아오는 보행.
    • 예: \((v_1, v_3), (v_3, v_3), (v_3, v_1)\)

  • 단순 사이클(simple cycle): 한 사이클에서 base 정점 외의 어느 정점도 중복하여 지나지 않는 것.

  • 루프(loop): 한 정점에서 자기 자신으로의 간선.
    • 예: \((v_3, v_3)\)

트리(Tree)

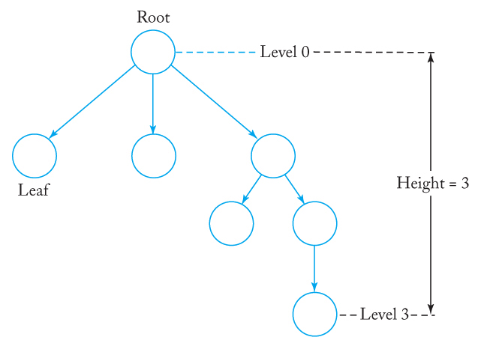
image

  • 트리는 그래프의 일종이다.
  • 트리는 사이클이 없으며, root라 불리는 하나의 구별되는 정점을 갖는 유향 그래프(directed graph)이다.
  • 루트에서 다른 모든 정점으로는 하나의 경로만이 존재한다.
  • 루트는 진입 간선(incoming edge)가 없다.
  • 트리는 진출 간선(outgoing edge)을 갖지 않는 정점들이 존재한다.
    • 이런 정점들을 leaves라 부른다.
  • 부모(parent): 정점 \(v_i\)에서 \(v_j\)로의 간선이 존재할 때, \(v_i\)를 부모라 한다.
  • 자식(child): 정점 \(v_i\)에서 \(v_j\)로의 간선이 존재할 때, \(v_j\)를 자식이라 한다.
  • 레벨(level): 루트에서 해당 노드까지의 간선의 개수.
  • 높이(height): 트리의 정점들 중 가장 큰 레벨을 갖는 정점의 레벨.
  • 각 레벨에 있는 노드에 순서를 부여하는 트리를 순서 트리(ordered tree)라 부른다.

증명 기법(Proof Techniques)

  • 귀납법(proof by induction)
  • 귀류법(proof by contradiction)