유로 문제(euro problem)
동전이 한 쪽으로 기울었다는 것을 증명하자
개요
- 이 문서는 [[/study/think-bayes]] 책 53~58쪽을 공부한 내용이다.
- David MacKay는 정보 이론, 추론, 학습 알고리즘 분야에 다음 문제를 제안했다.
가디언 지 2002년 1월 4일 금요일에 다음 통계가 게재되었다.
벨기에 1유로 동전으로 실험을 했는데, 축을 중심으로 250번 회전을 시켰을 때 앞면은 140회, 뒷면은 110회 나왔다. LSE(런던 경제 대학)의 교수 Barry Blight는 '내가 보기엔 좀 의심스럽다. 만약 동전이 한 쪽으로 기울어진 게 아니라면, 결과가 이렇게 치우칠 확률은 7% 미만이다'고 말했다. 하지만 이 데이터로 동전이 한 쪽으로 기울었다는 것을 증명할 수 있을까?
풀이
가설과 데이터 정의
- 가설 \(H_x\) : 앞면이 나올 확률이 0부터 100까지 중 \(x\%\) 이다.
- 즉, 101가지의 가설이 가능: \(H_0, \space H_1, \space ..., \space H_{100}\)
- 앞면이 나올 확률 : \(x \over 100\)
- 뒷면이 나올 확률 : \(100 - x \over 100\)
- 데이터
- 250번 회전을 시켰더니 앞면 140회, 뒷면 110회가 나왔다.
표로 정리해보면 다음과 같을 것이다.
| 식 | 설명 | 값 |
|---|---|---|
| \(p(H_0)\) | 앞면이 나올 확률이 0인 가설일 확률 | 0 |
| \(p(H_1)\) | 앞면이 나올 확률이 \(1 \over 100\)인 가설일 확률 | \(1 \over 101\) |
| … | … | … |
| \(p(H_{100})\) | 앞면이 나올 확률이 \(100 \over 100\)인 가설일 확률 | \(1 \over 101\) |
| \(p(D \mid H_0)\) | 가설 \(H_0\)인 상태에서, 앞면 140회, 뒷면 110회가 나올 확률 | \(\left(\frac{0}{100}\right)^{140}\left(\frac{100}{100}\right)^{110}\) |
| \(p(D \mid H_1)\) | 가설 \(H_1\)인 상태에서, 앞면 140회, 뒷면 110회가 나올 확률 | \(\left(\frac{1}{100}\right)^{140}\left(\frac{99}{100}\right)^{110}\) |
| … | … | … |
| \(p(D \mid H_{100})\) | 가설 \(H_100\)인 상태에서, 앞면 140회, 뒷면 110회가 나올 확률 | \(\left(\frac{100}{100}\right)^{140}\left(\frac{0}{100}\right)^{110}\) |
| \(p(D)\) | 문제의 동전을 던져 앞면 140회, 뒷면 110회가 나올 확률 | \(\sum_{n = 0}^{100}p(D \mid H_n)\) |
사후 확률을 계산하자
이제 각 가설별 사후 확률을 계산할 수 있다.
[[Bayes-theorem]]에 의해 사후 확률은 다음과 같다.
\[\begin{align} p(H_n \mid D) & = {p(H_n) \times p(D \mid H_n) \over p(D)} \\ & = {\frac{1}{101} \left(\frac{n}{100}\right)^{140}\left(\frac{100 - n}{100}\right)^{110} \over p(D)} \\ \end{align}\]손으로 직접 계산하기 번거로운 상태이므로 그냥 코딩을 하도록 하자.
다음은 ThinkBayes2의 eury.py를 참고하여 Javascript로 작성한 코드이다.
// hypos: 가설의 배열
// 가설의 배열을 돌며 같은 경우의 수 1을 부여한다
function init(hypos) {
const dict = {};
hypos.forEach((h) => {
dict[h] = 1;
});
return dict;
}
function update(dict, data) {
Object.keys(dict).forEach((hypo) => {
dict[hypo] = dict[hypo] * likelihood(data, hypo);
});
return normalize(dict);
}
// p(D | H_n)
function likelihood(data, hypo) {
const x = hypo;
if (data == 'H') {
return x/100.0;
}
return (100 - x)/100.0;
}
function range(start, size) {
return [...Array(size).keys()].map((n) => n + start);
}
// 모든 가설의 확률의 비율을 유지하며, 총합이 1이 되도록 정규화한다
function normalize(dict) {
const values = Object.values(dict);
const sum = values.reduce((a, b) => a + b);
const result = {};
Object.keys(dict).forEach((key) => {
result[key] = dict[key] / sum;
});
return result;
}
function main(max) {
const hypos = range(0, max);
let suite = init(hypos);
const datasetA = range(1, 140).map(() => 'H');
const datasetB = range(1, 110).map(() => 'T');
const dataset = datasetA.concat(datasetB);
dataset.forEach((coin) => {
suite = update(suite, coin);
});
Object.keys(suite).forEach((key) => {
console.log(key + '\t' + suite[key]);
});
}
main(101)
위의 코드를 실행한 결과를 복사하여…
$ node euro.js | pbcopy
엑셀에 붙여넣은 다음 차트를 그리면 다음과 같은 결과가 나온다.
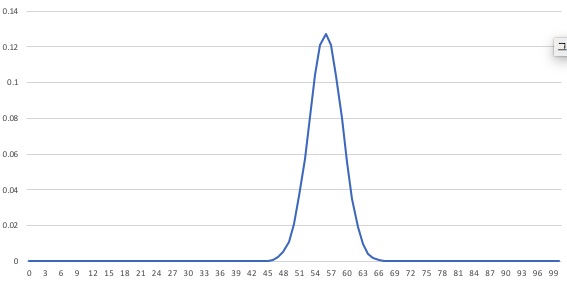
사후 확률 요약
가장 높은 확률의 값
위에서 실행한 결과 중 가장 큰 값을 갖는 가설을 찾아보면 0.127453180583913가 나온 \(H_{56}\)이라는 것도 알 수 있다.
약 12.745%라 할 수 있겠다.
\(H_{56}\)은 앞면이 나올 확률이 56%인 가설을 의미하는데,
앞면과 뒷면의 비율이 \(\frac{140}{250} = 0.56\) 이므로
동전을 던져 관측한 비율과 모수의 최대 우도 추정값이 일치했다고 할 수 있다.
평균(Mean)과 중간값(Median)
평균은 다음과 같이 구할 수 있다.
let mean = 0;
Object.keys(suite).forEach((key) => {
mean += key * suite[key];
});
console.log('mean : ' + mean);
실행해보면 다음과 같이 나온다.
mean : 55.95238095238094
중간값은 정 가운데에 위치하는 하나의 값을 구하면 되므로, 0과 100의 중간에 위치한 55의 값인 0.12116732716001365가 중간값이라 할 수 있다.
신뢰구간
이번에는 위에서 계산한 분포 목록을 사용하여 90% 신뢰구간을 구해보자.
5분위와 95분위 값을 계산하면, 90% 신뢰구간을 구할 수 있다.
이미 normalize를 했기 때문에 그대로 순서대로 더해주기만 하면 되겠다.
- 5분위 : 0~5% 에 해당하는 값을 모두 더해주면 된다.
- 95분위 : 0~95% 에 해당하는 값을 모두 더해주면 된다.
90% 신뢰구간은 다음과 같이 계산할 수 있다.
const keys = Object.keys(suite);
let p5 = 0;
let p5total = 0;
for(let i = 0; i < keys.length; i++) {
const val = keys[i];
const prob = suite[val];
p5total += prob;
if (p5total >= 0.05) {
p5 = val;
break;
}
}
let p95 = 0;
let p95total = 0;
for(let i = 0; i < keys.length; i++) {
const val = keys[i];
const prob = suite[val];
p95total += prob;
if (p95total >= 0.95) {
p95 = val;
break;
}
}
console.log({ '5%': p5, '95%': p95});
실행해보면 다음과 같은 결과가 나온다.
{ '5%': '51', '95%': '61' }
즉, 90% 신뢰구간은 (51, 61)이다.
문제의 동전은 평평한가?
이에 대해서는 \(H_{50}\)의 사후 확률을 조사해볼 수 있을 것이다.
위에서 계산했던 사후 확률 분포에서 50, 즉 동전이 완전히 공정할 경우의 확률은 0.020976526129544662 이다.
이는 약 2.09%에 해당한다.
사전 분포 범람(Swamping the priors)
위의 계산에서는 모든 가설에 대해 사전 분포로 똑같이 1을 부여했었다.
동전이 종이도 아니고… \(H_0\)과 \(H_{50}\)의 사전 확률이 1로 똑같다는 것은 납득하기 힘들다.
따라서 다음과 같은 사전 확률 부여를 고려해볼 수 있다.
| \(H_n\) | 사전 확률(normalize 전) |
|---|---|
| \(H_0\) | 0 |
| \(H_1\) | 1 |
| \(H_2\) | 2 |
| \(H_3\) | 3 |
| … | … |
| \(H_{49}\) | 49 |
| \(H_{50}\) | 50 |
| \(H_{51}\) | 49 |
| \(H_{52}\) | 48 |
| … | … |
| \(H_{99}\) | 1 |
| \(H_{100}\) | 0 |
코드로는 다음과 같이 init함수를 수정해주면 된다.
function init(hypos) {
const dict = {};
const half = parseInt(hypos.length / 2, 10) + 1;
for (var i = 0; i < half; i++) {
dict[i] = hypos[i];
}
for (var i = half; i < hypos.length; i++) {
dict[i] = 100 - hypos[i];
}
return dict;
}
특별한 것은 없고 0~50 사이에서는 \(H_n\)이 \(H_1\)보다 n 배 높은 확률을 갖게 하고, 그 이상에서는 반대로 줄어들도록 한 것이다.
이는 삼각 사전 확률이라 부른다. 그래프로 그리면 0에서 50까지는 1차 직선으로 쭉 올라가고, 그 이후부터는 쭉 내려가는데 아마도 그래프 모양 때문에 그렇게 부르고 있는 것 같다.
이를 실행해보면 다음과 같은 결과가 나온다. 대체로 비슷하다.
| 균등 사전 확률 | 삼각 사전 확률 | |
|---|---|---|
| 평균 | 55.95238095238094 | 55.743499438595045 |
| 중간값 | 0.12116732716001365 | 0.1239761099253328 |
| 90% 신뢰구간 | (51, 61) | (51, 61) |
| 최대 확률 | \(H_{56}\) 0.127453180583913 | \(H_{56}\) 0.12750972751803677 |
사전 확률을 완전히 다르게 부여하고 계산을 시작했는데 결과가 비슷하다.
이와 같이 데이터가 충분히 많은 경우 서로 다른 사전 확률로 시작해도 거의 동일한 사후 확률로 수렴하는 것을 사전 분포 범람(swamping the priors)이라 부른다.
Links
- [[Bayes-theorem]]
- [[/study/think-bayes]]
- [[Cromwell-s-rule]]