병합 정렬 (Merge Sort)

병합
- 구현
하향식(top down) 병합 정렬
상향식 (bottom up) 병합 정렬
예제 코드 전문
- 테스트 코드
성능
함께 읽기
참고문헌
주석

병합

TAOCP에서는 다음과 같이 병합을 설명한다.¹

TAOCP 3권. 5.2.4장. 195쪽. ↩

병합(merging) 또는 취합(collating)은 둘 이상의 순서 있는 파일들을 하나의 순서 있는 파일로 합치는 것을 말한다. 예를 들어 파일 503 703 765와 파일 087 512 677을 병합하면 087 503 512 677 703 765가 된다. 이를 수행하는 한 가지 간단한 방식은 두 파일에서 가장 작은 두 원소를 찾고 그 중 더 작은 것을 출력하는 과정을 반복하는 것이다.

\begin{matrix} {\begin{matrix} 503 & 703 & 765 087 & 512 & 677 \end{matrix} 087 & {\begin{matrix} 503 & 703 & 765 512 \end{matrix} 087503 & {\begin{matrix} 703 & 765 512 \end{matrix} 087503512 & {\begin{matrix} 703 & 765 \end{matrix} \end{matrix}

$\begin{align} & \begin{cases} 503 & 703 & 765 \\ \color{red}{087} & 512 & 677 \end{cases} \\ \\ \color{blue}{087} & \begin{cases} \color{red}{503} & 703 & 765 \\ 512 & \end{cases} \\ \\ 087 \ \color{blue}{503} & \begin{cases} 703 & 765 \\ \color{red}{512} & \end{cases} \\ \\ 087 \ 503 \ \color{blue}{512} & \begin{cases} \color{red}{703} & 765 \\ \ \end{cases} \\ \\ \end{align}$

로버트 세지윅은 다음과 같이 병합을 설명한다.²

알고리즘 [개정4판]. 2.2장. 269쪽. ↩

병합은 두 개의 정렬된 배열을 하나의 큰 정렬된 배열로 합치는 작업이다. 이 작업은 단순한 재귀적 방법으로 쉽게 구현된다. 즉, 배열을 정렬할 때, 그것을 반으로 나누어 각각의 절반에 대해서 재귀적으로 정렬을 수행하고, 다시 재귀적으로 정렬 결과를 병합한다. 앞으로 보게 되듯이, 병합 정렬의 가장 큰 장점 중 하나는 크기 $N$ 인 배열을 정렬하는 시간이 $N \log N$ 에 비례한다는 것이다. 대신 $N$ 에 비례하는 추가적인 메모리 공간을 소요한다는 것이 가장 큰 단점이다.

구현

다음은 세지윅의 알고리즘에 실린 예제 코드³

알고리즘 [개정4판]. 2.2장. 270쪽. ↩

를 참고하여 내가 java 언어로 작성한 코드다.

int[] aux;

/**
 * 주어진 a 배열의 sub 배열 a[lo..mid]와 sub 배열 a[mid+1..hi]를 병합합니다.
 *
 * @param a   배열
 * @param lo  첫번째 sub 배열 시작 인덱스
 * @param mid 첫번째 sub 배열 마지막 인덱스
 * @param hi  두번째 sub 배열 마지막 인덱스
 */
void merge(int[] a, int lo, int mid, int hi) {
  //  a[lo..hi]를 aux[lo..hi]에 복제
  for (int k = lo; k <= hi; k++) {
    aux[k] = a[k];
  }

  int i = lo;       // sub 배열 1 인덱스
  int j = mid + 1;  // sub 배열 2 인덱스

  // 다시 a[lo..hi]로 병합
  for (int k = lo; k <= hi; k++) {
    if (i > mid) {
      // sub 배열 1 인덱스가 마지막까지 갔다면 sub 배열 2의 값을 선택해 넣는다
      a[k] = aux[j++];
    } else if (j > hi) {
      // sub 배열 2 인덱스가 마지막까지 갔다면 sub 배열 1의 값을 선택해 넣는다
      a[k] = aux[i++];
    } else if (aux[j] < aux[i]) {
      // 두 sub 배열 헤드 중 작은 값을 선택해 넣는다
      a[k] = aux[j++];
    } else {
      // 두 sub 배열 헤드 중 작은 값을 선택해 넣는다
      a[k] = aux[i++];
    }
  }
}

이 메소드는 두 개의 정렬된 서브 배열을 병합하는 기능만을 갖고 있다.

하향식(top down) 병합 정렬

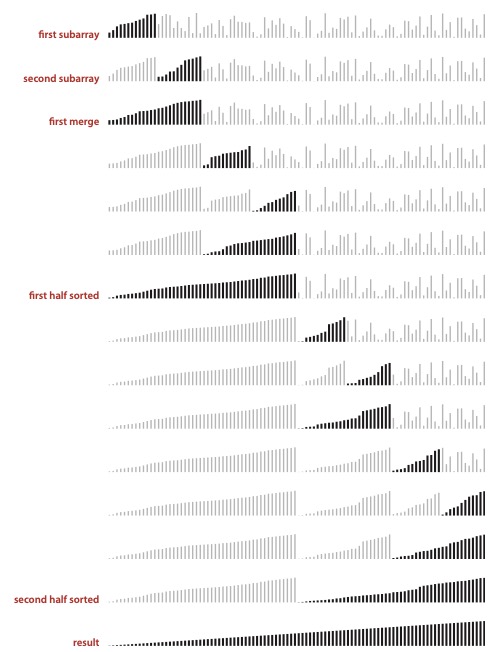
다음은 세지윅의 알고리즘에 수록된 하향식 머지 정렬의 이미지를 발췌한 것이다.

각 단계별로 '정렬된 서브 배열' 2개를 만들고 병합하는 과정을 반복하는 것을 볼 수 있다.

private int[] aux;

/**
 * 주어진 a 배열의 a[lo..hi] 구간을 정렬한다.
 *
 * @param a 배열
 */
void topDownMergeSort(int[] a) {
  aux = new int[a.length];
  topDownMergeSort(a, 0, a.length - 1);
}

/**
 * 주어진 a 배열의 a[lo..hi] 구간을 정렬한다.
 *
 * @param a  배열
 * @param lo 정렬 대상 시작 인덱스
 * @param hi 정렬 대상 마지막 인덱스
 */
void topDownMergeSort(int[] a, int lo, int hi) {
  if (hi <= lo) {
    return;
  }
  int mid = lo + (hi - lo) / 2;
  topDownMergeSort(a, lo, mid);     // 왼쪽 절반 정렬
  topDownMergeSort(a, mid + 1, hi); // 오른쪽 절반 정렬
  merge(a, lo, mid, hi);            // 결과 병합
}

상향식 (bottom up) 병합 정렬

상향식 병합 정렬은 작은 서브 배열을 여러 개 정렬해 놓고, 점점 서브 배열의 수를 반씩 줄여 나가는 방법이다.

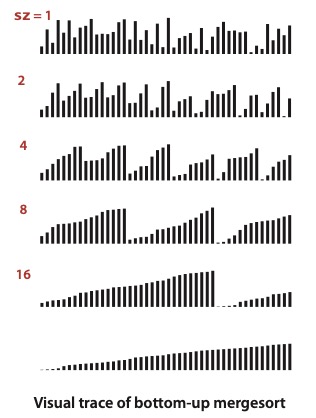
상향식 병합 정렬과 하향식 병합 정렬은 작업 순서만 다를 뿐, 복잡도는 차이가 거의 없다.

/**
 * 주어진 a 배열을 정렬한다.
 */
void bottomUpMergeSort(int[] a) {
  int N = a.length;
  aux = new int[N];
  for (int size = 1; size < N; size = size + size) {
    // size: 서브 배열의 크기
    for (int lo = 0; lo < N - size; lo += size + size) {
      // lo: 서브 배열의 인덱스
      merge(a, lo, lo + size - 1, Math.min(lo + size + size - 1, N - 1));
    }
  }
}

예제 코드 전문

다음은 위의 예제 코드 전문이다.

/**
 * 병합 정렬.
 */
public class MergeSort {
  private int[] aux;

  /**
   * 주어진 a 배열을 정렬한다.
   */
  void topDownMergeSort(int[] a) {
    aux = new int[a.length];
    topDownMergeSort(a, 0, a.length - 1);
  }

  /**
   * 주어진 a 배열의 a[lo..hi] 구간을 정렬한다.
   *
   * @param a  배열
   * @param lo 정렬 대상 시작 인덱스
   * @param hi 정렬 대상 마지막 인덱스
   */
  void topDownMergeSort(int[] a, int lo, int hi) {
    if (hi <= lo) {
      return;
    }
    int mid = lo + (hi - lo) / 2;
    topDownMergeSort(a, lo, mid);     // 왼쪽 절반 정렬
    topDownMergeSort(a, mid + 1, hi); // 오른쪽 절반 정렬
    merge(a, lo, mid, hi);            // 결과 병합
  }

  /**
   * 주어진 a 배열을 정렬한다.
   */
  void bottomUpMergeSort(int[] a) {
    int N = a.length;
    aux = new int[N];
    for (int size = 1; size < N; size = size + size) {
      // size: 서브 배열의 크기
      for (int lo = 0; lo < N - size; lo += size + size) {
        // lo: 서브 배열의 인덱스
        merge(a, lo, lo + size - 1, Math.min(lo + size + size - 1, N - 1));
      }
    }
  }

  /**
   * 주어진 a 배열의 sub 배열 a[lo..mid]와 sub 배열 a[mid+1..hi]를 병합합니다.
   *
   * @param a   배열
   * @param lo  첫번째 sub 배열 시작 인덱스
   * @param mid 첫번째 sub 배열 마지막 인덱스
   * @param hi  두번째 sub 배열 마지막 인덱스
   */
  void merge(int[] a, int lo, int mid, int hi) {
    //  a[lo..hi]를 aux[lo..hi]에 복제
    for (int k = lo; k <= hi; k++) {
      aux[k] = a[k];
    }

    int i = lo;       // sub 배열 1 인덱스
    int j = mid + 1;  // sub 배열 2 인덱스

    // 다시 a[lo..hi]로 병합
    for (int k = lo; k <= hi; k++) {
      if (i > mid) {
        // sub 배열 1 인덱스가 마지막까지 갔다면 sub 배열 2의 값을 선택해 넣는다
        a[k] = aux[j++];
      } else if (j > hi) {
        // sub 배열 2 인덱스가 마지막까지 갔다면 sub 배열 1의 값을 선택해 넣는다
        a[k] = aux[i++];
      } else if (aux[j] < aux[i]) {
        // 두 sub 배열 헤드 중 작은 값을 선택해 넣는다
        a[k] = aux[j++];
      } else {
        // 두 sub 배열 헤드 중 작은 값을 선택해 넣는다
        a[k] = aux[i++];
      }
    }
  }
}

테스트 코드

@DisplayName("MergeSort")
class MergeSortTest {
  @Nested
  @DisplayName("topDownMergeSort 메소드는")
  class Describe_topDownMergeSort {
    @Nested
    @DisplayName("정렬되지 않은 배열이 주어지면")
    class Context_with_unsorted_array {
      final int[] givenArray = new int[] {4, 2, 9, 187, 3, 5, 98};

      @Test
      @DisplayName("주어진 배열을 정렬한다")
      void it_sorts_array() {
        new MergeSort().topDownMergeSort(givenArray);

        for (int i = 1; i < givenArray.length; i++) {
          assertTrue(givenArray[i - 1] < givenArray[i]);
        }
      }
    }
  }

  @Nested
  @DisplayName("bottomUpMergeSort 메소드는")
  class Describe_bottomUpMergeSort {
    @Nested
    @DisplayName("정렬되지 않은 배열이 주어지면")
    class Context_with_unsorted_array {
      final int[] givenArray = new int[] {4, 2, 9, 187, 3, 5, 98};

      @Test
      @DisplayName("주어진 배열을 정렬한다")
      void it_sorts_array() {
        new MergeSort().bottomUpMergeSort(givenArray);

        for (int i = 1; i < givenArray.length; i++) {
          assertTrue(givenArray[i - 1] < givenArray[i]);
        }
      }
    }
  }
}

성능

최악의 경우 시간 복잡도	$\Theta (n \log n)$
최선의 경우 시간 복잡도	$\Theta (n \log n)$
평균적인 경우 시간 복잡도	$\Theta (n \log n)$
최악의 경우 공간 복잡도	$\Theta(n)$ 부가 공간

병합 정렬에서 정렬 대상 배열은 두 개의 서브 배열로 나뉘어 재귀적으로 해결된다.
서브 문제를 푼 다음 두 서브 문제의 결과를 비교하면서 병합한다.

따라서 병합 정렬의 재귀는 다음과 같다.

T (n) = 2 T (n / 2) + Θ (n)

$T(n) = 2T(n/2) + \Theta(n)$

여기에 마스터 정리를 사용하면, $T(n) = \Theta(n \log n)$ 이 된다.

마스터 정리를 적용하는 과정이 어떤지 자세히 살펴보자.

마스터 정리 재귀 관계식은 다음과 같다.

T (n) = a T (n / b) + Θ (n^{k} {log}^{p} n)

$T(n) = aT(n/b) + \Theta(n^k \log^p n)$

그리고 $a \ge 1, b \gt 1, k \ge 0$ 이고, $p$ 는 실수여야 한다.

병합 정렬의 모양이 다음과 같으므로…

T (n) = 2 T (n / 2) + Θ (n)

$T(n) = 2T(n/2) + \Theta(n)$

$a = 2, b = 2, k = 1, p = 0$ 이다.

$a = b^k$ 인 경우에 해당되며, $p \gt -1$ 이므로, 마스터 정리 2-a 를 사용할 수 있다.

마스터 정리 2-a는 다음과 같다.

T (n) = Θ (n^{{log}_{b}^{a}} {log}^{p + 1} n)

$T(n) = \Theta(n^{ \log_b^a } \log^{p+1} n )$

여기에 $a = 2, b = 2, k = 1, p = 0$ 를 대입하면 다음과 같이 된다.

\begin{matrix} T (n) & = Θ (n^{{log}_{2}^{2}} {log}^{1} n) = Θ (n log n) \end{matrix}

$\begin{align} T(n) & = \Theta(n^{ \log_2^2 }\log^{1} n ) \\ & = \Theta(n \log n ) \\ \end{align}$

성능 향상

크기가 15이하인 서브 배열을 정렬할 때에는 재귀적으로 정렬하지 않고 삽입 정렬 (Insertion Sort)를 사용하면 일반적인 병합 정렬 구현보다 10% ~ 15% 정도 성능이 개선된다고 한다.^{4
알고리즘 [개정4판]. 2.2장. 274쪽. ↩ ↩²}
두 서브 배열이 서로 겹치지 않을 때(비교할 필요가 없을 때) 정렬을 생략하면 성능을 향상시킬 수 있다.
- a[mid] $\le$ a[mid+1] 인지 확인하면 된다.

하향식 병합 정렬의 비교 연산 횟수

명제 F

하향식 병합 정렬은 크기 $N$ 인 배열을 정렬할 때 $\sim \frac{1}{2} N \lg N ... N \lg N$ 사이의 횟수로 비교 연산을 수행한다. ⁵
알고리즘 [개정4판]. 2.2장. 271쪽. ↩

이는 다음과 같이 증명할 수 있다.

크기 N인 배열을 정렬하는 데 필요한 비교 연산 횟수 = C(N)
- $C(0) = 0$ .
- $C(1) = 0$ .

$\def\ceil#1{\lceil #1 \rceil} \def\floor#1{\lfloor #1 \rfloor} \def\frfr#1{\{ #1 \}}$

구현 코드는 다음과 같은 구조를 갖고 있었다.

왼쪽 절반을 정렬. 절반을 정렬하므로 비교 횟수는 $C( N/2 )$ .
오른쪽 절반을 정렬. 절반을 정렬하므로 비교 횟수는 $C( N/2 )$ .
왼쪽 절반과 오른쪽 절반을 병합. 정렬 없이 병합만 하므로 비교 횟수는 최소 N/2, 최대 N.
- $N/2$ 인 경우: 왼쪽 절반의 모든 원소가 오른쪽 절반보다 작다면, 왼쪽 절반이 머지된 이후 오른쪽 절반은 비교하지 않아도 된다.

이 구조를 참고해 식으로 옮겨보자.

비교 횟수의 상한

$C(N) \le C( \ceil{ N / 2 } ) + C( \floor{ N / 2 } ) + N \tag{1}\label{1}$

비교 횟수의 하한

$C(N) \ge C( \ceil{ N / 2 } ) + C( \floor{ N / 2 } ) + \floor{ N / 2 } \tag{2}\label{2}$

이제 $N = 2^n$ 인 경우에 한해서 증명해 보자.

N=2n 이므로 N/2=2n−1 이다.
- $\ceil{ N /2 } = 2^{n-1}$
- $\floor{ N /2 } = 2^{n-1}$

이를 식 $\eqref{1}$ 에 대입해 보자. 맞닿는 경우를 생각하는 것이므로 부등호는 등호로 바꾼다.

$\begin{align} C(N) & = C( \ceil{ N / 2 } ) + C( \floor{ N / 2 } ) + N \\ \\ C( 2^n ) & = C( 2^{n-1} ) + C( 2^{n-1} ) + 2^n \\ & = 2C( 2^{n-1} ) + 2^n \\ \end{align}$

양 변을 $2^n$ 으로 나눠주자.

$\begin{align} {C( 2^n ) \over 2^n} & = {2C( 2^{n-1} ) \over 2^n } + {2^n \over 2^n} \\ & = \color{red}{C( 2^{n-1} ) \over 2^{n-1} } + 1 \\ \tag{4}\label{4} \end{align}$

이 때, ${C( 2^n ) \over 2^n} = {C( 2^{n-1} ) \over 2^{n-1} } + 1$ 이므로 $\color{red}{C( 2^{n-1} ) \over 2^{n-1}} = {C( 2^{n-2} ) \over 2^{n-2} } + 1$ 라는 것도 어렵지 않게 알 수 있다.

이걸 $\eqref{4}$ 에 대입하면 다음과 같이 된다.

$\begin{align} {C( 2^n ) \over 2^n} & = \left( {C( 2^{n-2} ) \over 2^{n-2} } + 1 \right) + 1 \\ & = {C( 2^{n-2} ) \over 2^{n-2} } + 2 \\ \end{align}$

이 과정을 $n-1$ 번 반복하면 다음과 같이 될 것이다.

$\begin{align} {C( 2^n ) \over 2^n} & = {C( 2^{0} ) \over 2^{0} } + n \\ & = C( 1 ) + n \\ & = n \\ \end{align}$

양 변에 $2^n$ 을 곱해주자.

$C( 2^n ) = 2^n \times n$

그런데 $N = 2^n$ 이고 $\lg N = n$ 이므로 다음과 같이 정리할 수 있다.

$\begin{align} C( N ) & = 2^n \times n \\ & = N \lg N \\ \end{align}$

그러므로 $C(N) \le N \lg N$ 이다.

그리고 $\eqref{2}$ 의 경우

${C( 2^n ) \over 2^n} = {C( 2^{n-1} ) \over 2^{n-1} } + \frac{1}{2}$

이므로, 다음과 같이 정리되고…

$\begin{align} C( 2^n ) & = 2^n \times {n \over 2} C( N ) & = \frac{1}{2} N \lg N \end{align}$

그러므로 비교 횟수 $C(N)$ 은 다음과 같이 요약된다.

$\frac{1}{2} N \lg N \le C(N) \le N \lg N$

하향식 병합 정렬의 배열 접근 횟수

비교 연산 횟수를 구하는 것은 계산이 좀 필요했지만, 배열 접근 횟수는 간단하게 알아낼 수 있다.

명제 G

하양식 병합 정렬은 크기 $N$ 인 배열을 정렬할 때 최대 $6N \lg N$ 번의 배열 접근을 한다.

증명: 각 병합 단계는 최대 $6N$ 번의 배열 접근을 한다(복제에 $2N$ 번, 이동에 $2N$ 번, 그리고 비교를 위해 최대 $2N$ 번). 이 결과는 명제 F의 논증에서도 마찬가지로 도출된다.⁴
알고리즘 [개정4판]. 2.2장. 274쪽. ↩ ↩²

주의

병합 정렬은 중복 키가 존재하는 경우, 그 어떤 입력 분포에 대해서도 최적 성능을 보증하지 않는다.⁶
알고리즘 [개정4판]. 2.3장. 297쪽. ↩

함께 읽기

빅 오 표기법(Big O notation)

참고문헌

The art of computer programming 3 정렬과 검색(개정2판) / 도널드 커누스 저 / 한빛미디어 / 초판 2쇄 2013년 02월 10일
알고리즘 [개정4판] / 로버트 세지윅, 케빈 웨인 저/권오인 역 / 길벗 / 초판발행 2018년 12월 26일

주석

TAOCP 3권. 5.2.4장. 195쪽. ↩
알고리즘 [개정4판]. 2.2장. 269쪽. ↩
알고리즘 [개정4판]. 2.2장. 270쪽. ↩
알고리즘 [개정4판]. 2.2장. 274쪽. ↩ ↩²
알고리즘 [개정4판]. 2.2장. 271쪽. ↩
알고리즘 [개정4판]. 2.3장. 297쪽. ↩